zacc
- 8
- 0
Homework Statement
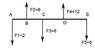
The attached figure shows a weightless bar with several forces applied to it (all in New). The distances are as follow: AB=6m, BC=1m and CD=3m. The question is to calculate DE so there is equilibrium.
Homework Equations
ƩM=0 (Rotational equilibrium) (Counterclockwise moments are +)
The Attempt at a Solution
I have been going around this problem for a while. I tried to apply the equilibrium condition:
ƩM=0 where M are the moments. But I get different answers depending on which point I choose to calculate the moments:
A: 0x2+6x6-8x7+10x12-(10+DE)6=0 This gives DE=6.66
D: 2x10-4x6+8x3-6DE=0 This gives DE=3,33 (the correct answer according to the book)
C: 2x7-6x1+3x12-(3+DE)6=0 This gives DE=4.3
So, I am a little lost here.
The only thing that I can notice is that the system is not at translational equilibrium as:
ƩF ≠ 0 (forces pointing up are +)
In fact, if I make F5=8 N so that ƩF=0 then DE comes to the same answer (2.5) no matter which point I use to calculate the moments. This is what I was expecting before as well.
Could please someone help me to understand these results? Thanks for the help!
Attachments
Last edited: