jmoney
- 2
- 0
I'm trying to get my head around this scenario:
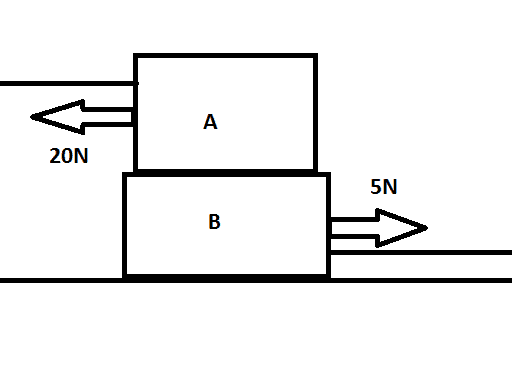
The blocks are at rest, despite the tension forces acting on them.
It is obvious that the static friction acting on A from B is 20N to the right for A to remain at rest (the max might be a lot higher).
But does this produce an equal and opposite reaction on B? It seems to me that the static friction should have some reaction... but it also seems silly to think that A could exert a leftward force on B when A isn't even moving.
Are the forces acting on B (before possible floor friction)
20N <--- B --> 5N or just B--->5N
Thank you, and I hope I have been clear enough! This is my first post on this forum.
The blocks are at rest, despite the tension forces acting on them.
It is obvious that the static friction acting on A from B is 20N to the right for A to remain at rest (the max might be a lot higher).
But does this produce an equal and opposite reaction on B? It seems to me that the static friction should have some reaction... but it also seems silly to think that A could exert a leftward force on B when A isn't even moving.
Are the forces acting on B (before possible floor friction)
20N <--- B --> 5N or just B--->5N
Thank you, and I hope I have been clear enough! This is my first post on this forum.