dhc107
- 3
- 0
Homework Statement
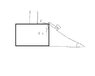
If i have a block that is d distance back from a slope, and I have cable coming out of the block (lets assume at ground level) that goes over to a fulcrum at the ledge of an incline of angle theta down to a block of mass m. What is the downward force at the fulcrum point?
2. Attempt at a solution
I can find the force of the string as m*g*sin(theta)
Last edited: