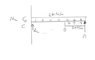
The discussion revolves around solving a beam deflection problem using the superposition method, with specific values for reactions and moments provided. The original poster struggles with calculating deflection at point A due to a distributed load that does not cover the entire beam. Participants suggest adding fictitious forces to complete the superposition and emphasize the need for the poster to show their working for better assistance. There is uncertainty about how to apply deflection equations from a table when the load is not uniformly distributed. The conversation highlights the complexity of using superposition for this type of beam problem.