Statics - Centroid of a 2-D figure

[into space]

Homework Statement

Problem

Homework Equations

Area of a semi-circle, area of a semi-sector of a circle, centroid of a semi-circle, centroid of a sector, general equation for centroid of a plate:

(X-Bar) * \SigmaArea = \Sigma(x-bar * Area)

The Attempt at a Solution

Attempt. I tried my best with the handwriting.

I forgot to write it down on the link above, but what I tried to do was subtract the area of the smaller semi-circle from the area of the larger-semi-circle and get an Area Q, then subtract Q by the area of the two semi-sectors.

I feel I am leaving something out with the sectors. I think it has to do with the centroids of the semi-sectors because the answer has a cosine in it and the only place where I can find a trig function is the x-coordinate for the centroid of a sector, but since the overall X-coordinate for the figure is 0, I don't know how to approach this.

 

[ehild]

What is the definition for the centroid? Have you learned the definition using integrals?

Would you please type in your attempt of solution.

ehild

 

[into space]

Hi ehild, thanks for taking the time to look at my question

What is the definition for the centroid? Have you learned the definition using integrals?

Would you please type in your attempt of solution.

ehild

A centroid is the center of gravity of a figure. The formula for the centroid via integrals is:

X-bar = (integral of x dA)/Area

Y-bar = (integral of y dA)/Area

Where the x is the distance from the y-axis to the element, and y is the distance from the x-axis to the element.

The work I've shown is tabulated which is why I chose not to write it out, but I'll do my best to explain it:

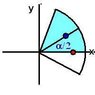
What the figure is is a little less than half a donut, depending on what alpha is. Separating this partial donut into other geometric figures yields:
1 larger half-circle
1 smaller half-circle
2 partial sectors of a circle

If I subtract the Area of the larger semi-circle and the smaller semi-circle, I get a half-donut, and if I subtract it further by the Area of the 2 partial sectors of a circle, I get the Area of the figure in question (less than half a donut).

The formulas for the Area and centroid of the semi-circle respectively are:
A = .5*pi*(r^2)

Y-Bar = (4r)/(3*pi)

The Y-bar because is zero and lies on the y-axis, and where r is the radius.

The formulas for the Area and centroid of the semicircle

The formulas for the Area and centroid of the semi-sectors respectively are:
A = (alpha(r^2))/2

X-Bar = (2*r*sin(alpha))/(3alpha)

where alpha is 1/2 the angle of the sector.

The total area of the figure is given by the subtraction of the areas of all these figures, which is:

Total A= .5*pi*(r2)^2 - .5*pi*(r1)^2 - alpha(r2)^2

where r1 is the radius of the smaller semi-circle and r2 is the radius of the larger semi-circle.

If the overall Y-bar or y-coordinate of the centroid of the figure is found by the equation:

Y-bar = sum of the y-bar centroids of each element multiplied by each individual area/total area

the y-coordinates of the elements multiplied by their respective areas are:
For the larger semi-circle: y-bar * A = (.5*pi*(r2)^2)*((4(r2))/(3*pi))
y-bar * A = (2/3) * (r2)^3

For the smaller semi-circle: y-bar * A = (.5*pi*(r1)^2)*((4(r1))/(3*pi))
y-bar * A = (2/3) * (r1)^3

Since the Areas of these figures are being subtracted from each other, their y-bar*Areas must too be subtracted:
Sum of y-coordinate Areas = (2/3)((r2)^3-(r1)^3)

The overall Y-bar coordinate of the centroid of this figure is found by dividing the sum of the y-coordinate areas by the total area of the figure, or:

Y-bar = ((2/3)((r2)^3-(r1)^3))/(.5*pi*(r2)^2 - .5*pi*(r1)^2 - alpha(r2)^2)

Which is my final answer to this question. The correct answer is:

Y-bar = ((2/3)((r2)^3 - (r1)^3)(2cos(alpha)))/(((r2)^2 - (r1)^2)(pi - 2alpha))

 

[ehild]

I think you used a wrong expression for the centroid of the sectors. The formula gives the distance of the centroid from the centre. You need the y coordinates.
Why don't you use the integral definition to get the centroid? It is very simple in polar coordinates. You know that dA= r dr dθ, so
determine the integral( sin(theta)r² dθ dr) from θ =α to θ=π-α and r=R₁ to r=R₂, and divide by the total area.

ehild

 

[into space]

I think you used a wrong expression for the centroid of the sectors. Why don't you use the integral definition to get the centroid? It is very simple in polar coordinates. You know that dA= r dr dθ, so
determine the integral( sin(theta)r² dθ dr) from θ =α to θ=π-α and r=R₁ to r=R₂, and divide by the total area.

ehild

I'm unsure of how to go about solving an integral when there is a dr and a dθ. Are you using double integrals? Because we haven't learned that yet.

 

[ehild]

Yes, it is double integral. Have you learned simple ones? Because this double integral is an integral with respect to the angle (here comes in the cosine) then the result integrated with respect to the radius.

This method you applied is very complicated. But you must use it if you do not know how to integrate.
Check your formula for the centroid of the sector. What does it mean? You denoted it with x-bar. But you need the y coordinate of this centroid.

ehild

 

[jhae2.718]

I'm unsure of how to go about solving an integral when there is a dr and a dθ. Are you using double integrals? Because we haven't learned that yet.

For a double integral like \int_{r_1}^{r_2}\!\!\!\! \int_{\theta_1}^{\theta_2} f(\theta) g(r) d\theta dr, take \int_{\theta_1}^{\theta_2} f(\theta})g(r) d\theta holding r constant and then take \int_{r_1}^{r_2}of the result dr.

 

[into space]

Yes, it is double integral. Have you learned simple ones? Because this double integral is an integral with respect to the angle (here comes in the cosine) then the result integrated with respect to the radius.

This method you applied is very complicated. But you must use it if you do not know how to integrate.
Check your formula for the centroid of the sector. What does it mean? You denoted it with x-bar. But you need the y coordinate of this centroid.

ehild

The problem I have is the formula for a circular sector has the middle of the sector resting on the x-axis, with both angles (alpha) equally above and below the x-axis. This makes the y-bar for the sector centroid 0. Here's a picture hopefully describing it better:
Here

There are two sectors in the problem, and they are both cut in half, which means they have an x and a y-bar as the centroid instead of just sitting in the middle of the axis. I need to know the y-bar of half of a sector in order to multiply that number by its area and compare it with the rest of the weights of the other elements.

 

[into space]

For a double integral like \int_{r_1}^{r_2}\!\!\!\! \int_{\theta_1}^{\theta_2} f(\theta) g(r) d\theta dr, take \int_{\theta_1}^{\theta_2} f(\theta})g(r) d\theta holding r constant and then take \int_{r_1}^{r_2}of the result dr.

Ok, just to make sure I'm doing this right, the end result of the double integral of sin(θ)*(r^2) dθ dr from θ = alpha to θ = (pi - alpha) and r = r1 to r=r2 is:

[cos(alpha)*r^{3}_{2}*(1/3) - cos (pi - alpha)*r^{3}_{2}*(1/3)] - [cos(alpha)*r^{3}_{1}*(1/3) - cos (pi - alpha)r^{3}_{1}*(1/3)]

 

[jhae2.718]

That's what I get.

 

[into space]

that's what i get.

Ok, dividing that by the total area which is:

A = .5(pi*(r2)^2 - pi*(r1)^2 - 2alpha(r2)^2)

And recognizing from trig identities that cos (pi - alpha) = -cos(alpha)

the equation is now:

[(r2)^3 - (r1)^3][2cos(alpha)]/[pi*(r2)^2 - pi*(r1)^2 - 2alpha(r2)^2]

My answer differs from the book's answer in the denominator, where there should be a +2alpha(r1)^2 added in the denominator which will allow the denominator to be factored into:

[(r2)^2 - (r1)^2][pi - 2alpha]

This means I had to calculate the area for a sector of a circle defined by r1 and r2, not just r2. The total area would then be:

(big semi-circle) - (little semi-circle) - (larger sector) - (smaller sector)

Why does the smaller sector make a difference? Why isn't:

(big semi-circle) - (little semi-circle) - (larger sector)

correct?

 

[jhae2.718]

(big semi-circle) - (little semi-circle) - (larger sector)

If you only do this, you are subtracting the area of the small sector twice (in the small semicircle and in the larger sector). What you need is: (big semicircle - small semicircle - 2(big sector - small sector))=(big semicircle - small semicircle -2*big sector + 2*small sector)

See this:

Also, what happened to the 1/2 in the area expression and the 1/3 from your integrand?

 

[into space]

If you only do this, you are subtracting the area of the small sector twice (in the small semicircle and in the larger sector). What you need is: (big semicircle - small semicircle - 2(big sector - small sector))=(big semicircle - small semicircle -2*big sector + 2*small sector)

Huh.

The way I'm thinking of it is like this. The area of the large sector is shaded in blue in this picture.

The area of the small sector is shaded in yellow here.

And the area of he combined sectors is overlapped in green here.

Wouldn't it be redundant to include the smaller yellow sector because it is just a scaled down version of the larger blue sector?

 

[jhae2.718]

See the image I added to my previous post.

 

[into space]

See this:
View attachment 33154

Also, what happened to the 1/2 in the area expression and the 1/3 from your integrand?

Makes perfect sense now. Thank you.

And the 1/2 was on the bottom so I flipped it up to the top as a 2 then brought the 1/3 out and it became 2/3.

 

[jhae2.718]

Makes perfect sense now. Thank you.

Glad to help with the double integral part; ehild did the hard part, though.

And the 1/2 was on the bottom so I flipped it up to the top as a 2 then brought the 1/3 out and it became 2/3.

Either I misread, or you forgot to include that here, then:

the equation is now:

[(r2)^3 - (r1)^3][2cos(alpha)]/[pi*(r2)^2 - pi*(r1)^2 - 2alpha(r2)^2]

That should be pretty much everything then?

 

[into space]

Glad to help with the double integral part; ehild did the hard part, though.

Either I misread, or you forgot to include that here, then:

That should be pretty much everything then?

Haha you're right, I kind of got ahead of myself in anticipation of solving a problem I've been working on for more than four hours. And yes, thank you ehild for the help as well.

Though I know now how to solve this problem using double integrals, I really wanted to know how to solve it with decomposition of geometric figures like the initial way I did. I guess this problem is only really meant to be solved one way.

 

[jhae2.718]

Though I know now how to solve this problem using double integrals, I really wanted to know how to solve it with decomposition of geometric figures like the initial way I did. I guess this problem is only really meant to be solved one way.

From a practical perspective, using polar coordinates and double integrals is far easier.

However, it's not too difficult to break it up into geometric figures and then find the CM, just more work.

So, the problem can be solved in more than one way. Some are easier than others.

 

[ehild]

Hi Everybody, I just woke up, (it is 5 am here) and I see, Jhae2 has thought double integral to you, Into space. Good job!
Now the other way solving this problem: See the picture. You were given the x coordinate of the horizontal centroid of angle 2α. Now it is α/2 below and above the x axis. For the horizontal one, you have to replace the angle α by α/2. So the centroid (red dot) is at
d=4r/3* sin(α/2)/(α) distance from the origin and A=r^2*α/2 .

Now you turn the sector by α/2. The centroid gets into the position of the blue dot. Its y coordinate is

y_c=d*sin(α/2)=4r/3 * sin²(α/2)/a

Using the identity sin²(α/2)=(1-cos(α))/2

y_c=2r/3 (1-cos(α))/α.

Now you can go on with the piecewise calculation.

ehild

 

[into space]

And so the monster of the problem is defeated. Again, thanks for all the help you two. If this problem comes up on a test, I'll blast it out of the water. :)