EtherealMonkey
- 41
- 0
The problem statement:
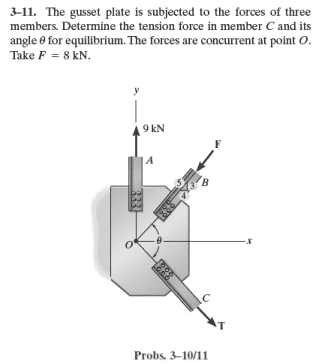
My relevant equation:
\phi will be the angle between the X axis and F_{CO}
\theta = \phi + \arcsin\left(\frac{3}{5}\right)
My attempt at a solution:
\Sigma F_{x} = 0:
F_{CO}\cos\phi - F_{BO}\frac{4}{5} = 0
F_{CO} = \frac{F_{BO}\frac{4}{5}}{\cos\phi}
\Sigma F_{y} = 0:
F_{AO} - F_{BO}\frac{3}{5} - F_{CO}\sin\phi = 0
Combining terms and substituting the equation found for \Sigma F_{x} = 0 into \Sigma F_{x} = 0:
F_{AO} - \frac{3}{5}F_{BO} - \frac{4}{5}F_{BO}\tan\phi = 0
9kN - \frac{3}{5}8kN - \frac{4}{5}8kN\tan\phi = 0
\phi = \arctan\left(\left(9+\frac{24}{5}\right)*\frac{5}{32}\right)
\phi = 65.12^{\circ}
\theta = 102^{\circ}
The published value of \theta:
\theta = 70.1^{\circ}
I don't know what I did wrong.
TIA for any response.
My relevant equation:
\phi will be the angle between the X axis and F_{CO}
\theta = \phi + \arcsin\left(\frac{3}{5}\right)
My attempt at a solution:
\Sigma F_{x} = 0:
F_{CO}\cos\phi - F_{BO}\frac{4}{5} = 0
F_{CO} = \frac{F_{BO}\frac{4}{5}}{\cos\phi}
\Sigma F_{y} = 0:
F_{AO} - F_{BO}\frac{3}{5} - F_{CO}\sin\phi = 0
Combining terms and substituting the equation found for \Sigma F_{x} = 0 into \Sigma F_{x} = 0:
F_{AO} - \frac{3}{5}F_{BO} - \frac{4}{5}F_{BO}\tan\phi = 0
9kN - \frac{3}{5}8kN - \frac{4}{5}8kN\tan\phi = 0
\phi = \arctan\left(\left(9+\frac{24}{5}\right)*\frac{5}{32}\right)
\phi = 65.12^{\circ}
\theta = 102^{\circ}
The published value of \theta:
\theta = 70.1^{\circ}
I don't know what I did wrong.
TIA for any response.
Last edited: