Statics: force to open a door on 2 rollers given friction

Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
Sign up Log in
3 replies · 3K views
SoylentBlue
Messages
50
Reaction score
8

Homework Statement


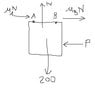
We have a 200-LB door hanging from 2 rollers, A & B, which are 5 feet apart. Coeffs of friction for A and B are .15 and .25, respectively. A force P is applied to the door. How big must it be to move the door to the left?[/B]

Homework Equations

The Attempt at a Solution


I have included a FBD. The downward force is the 200LBs, so the normal force would be 200, or 100 at each roller. That's reasonable, since the whole thing is symmetrical. The forces in x direction are P (to the left) and the total of muAN and muBN to the right.
So here we go:
Sum of forces in x: -P + (.15)(100) + (.25)(100) = 0
This yields a value of 40 for P. The book's answer is 45.5

Hmmm...been struggling with this for a week. Not sure where I made a wrong turn. Any help appreciated. Thank you.:biggrin:

[/B]
 

Attachments

  • Prob816FBD.jpg
    Prob816FBD.jpg
    6 KB · Views: 556
  • Prob816.jpg
    Prob816.jpg
    49.1 KB · Views: 641
Physics news on Phys.org
SoylentBlue said:
The downward force is the 200LBs, so the normal force would be 200, or 100 at each roller. That's reasonable, since the whole thing is symmetrical

The pull force creates a moment about B so the downward force at A will be greater than 100.
You'll have to assume C is directly below B.
 
Thank you thank you thank you for pointing me in the right direction. Your answer was perfect--just a hint, without giving the answer away.
As soon as I saw your reply, I actually said out loud "D'Oh!" I am embarrassed that I did not see something so obvious.:H Ok, in my defense, I am still a student and still learning.

Anyway, for anyone else struggling with this, here is how it is solved. Note that we are looking at problem 8.16, in which the force pushes to the left, not to the right.Sum of forces about B: -6P + 2.5(200) – 5NA=0

Sum of forces in x: -P + .15NA + .25NB=0

Sum of forces in y: -200 + NA + NBEasy mistake to make: assuming NA and NB are equal. They are not!

OK, 3 equations with 3 unknowns, which is solvable. I won’t bore you with grunt-work.

NA=45.5

NB=154.5

Then P is 45.5, which agrees with the book’s answer.

Thank you again:smile: