newbphysic
- 39
- 0
Determine the resultant internal loadings acting on the cross section
at C of the cantilevered beam
http://imgur.com/Q4ZUTOq
1. Homework Statement
F = 270 N/m
ΣV = 0
ΣM = 0
ΣN = 0
section CB[/B]
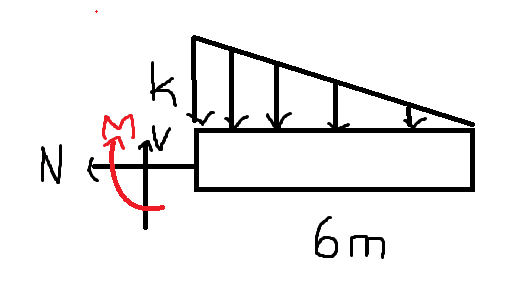
k/6 = 270/9
k = 180 N/m
resultant force = area under the curve = 1/2 * 180 * 6 = 540 N
ΣN = 0
-N = 0
N = 0
ΣV = 0
V - resultant = 0
v = resultant = 540 N
How can i find M ?
at C of the cantilevered beam
http://imgur.com/Q4ZUTOq
1. Homework Statement
F = 270 N/m
Homework Equations
ΣV = 0
ΣM = 0
ΣN = 0
The Attempt at a Solution
section CB[/B]
k/6 = 270/9
k = 180 N/m
resultant force = area under the curve = 1/2 * 180 * 6 = 540 N
ΣN = 0
-N = 0
N = 0
ΣV = 0
V - resultant = 0
v = resultant = 540 N
How can i find M ?