papasmurf
- 21
- 0
Could someone please check this for me? I attached a rough free body diagram of the whole frame. Any help is appreciated.
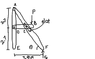
The member ACF of the frame loaded as shown is connected to member BCD by means of a smooth peg and slot C with force P = 930 N at point D. Determine the diameter of pin C in mm if the allowable shear stress is 150 MPa.
ƩM=0
ƩFY=0
ƩFX=0
τ=F/A
A=(pi/4)*d2
Taking ƩME=0, I have FY(4.8 m) - 930 N(3.6 m), FY=697.5 N.
Next, looking at member ACF, take ƩMA=0, where I have 697.5 N*(4.8 m) - C*cos(θ)*(2.4 m) - C*sin(θ)*(2.7 m), where θ=tan-1(5.4/4.8)=48.36°. Solving for C, I get C=926.79 N.
Shear is given by τ=F/A where F is the force acting on the pin C and A is the cross-sectional area of pin C. Solving for diameter I get 3.62 mm.
Homework Statement
The member ACF of the frame loaded as shown is connected to member BCD by means of a smooth peg and slot C with force P = 930 N at point D. Determine the diameter of pin C in mm if the allowable shear stress is 150 MPa.
Homework Equations
ƩM=0
ƩFY=0
ƩFX=0
τ=F/A
A=(pi/4)*d2
The Attempt at a Solution
Taking ƩME=0, I have FY(4.8 m) - 930 N(3.6 m), FY=697.5 N.
Next, looking at member ACF, take ƩMA=0, where I have 697.5 N*(4.8 m) - C*cos(θ)*(2.4 m) - C*sin(θ)*(2.7 m), where θ=tan-1(5.4/4.8)=48.36°. Solving for C, I get C=926.79 N.
Shear is given by τ=F/A where F is the force acting on the pin C and A is the cross-sectional area of pin C. Solving for diameter I get 3.62 mm.
Attachments
Last edited: