Statics problem, analysis of a frame

[yaro99]

Homework Statement

Homework Equations

ƩF_y=0
ƩF_x=0
ƩM=0

The Attempt at a Solution

The weight of the wire is 500*16=8000lb

I isolated each part of the system:

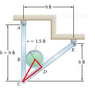
Using a force triangle on the cross section of the wire, knowing it is a 345 triangle:
8000/4=B/3=D/5
B=6 kips
D=10 kips

I wrote equations for members ABC and CDE:

for ABC:
ƩM_A = 6*d₁ + 9*C_x = 0

for CDE:
ƩM_E = 10*d₂ - 6*C_x + 8*C_y = 0

d₁ and d₂ are the vertical distance from A to B, and the diagonal distance from D to E, respectively. This is what I had trouble finding.
I tried using similar triangles:

5/8 = a/10 = (3+b)/6
b=0.75ft
d₂=6.25ft

Since b is 0.75, d₁ = 9 - 6 + 1.5 + 0.75 = 5.25ft

Plugging these into the above equations, I get Cx = 3.5kips, and Cy = 10.4 kips, which are not the right answers.

 

[Simon Bridge]

I would have expected Cx and Ex to point the other way to your diagram.
I think you may need to revisit the distances to the contact points (pipe to frame).
If you put point P at the center of the pipe, then what do you notice about the triangles CBP and CDP, and, therefore the relative lengths. You know the radius of the pipe and the angle BCP.

note: suggest you use d=|CD| and b=|CB| to ease typing ;)

 

[TSny]

for ABC:
ƩM_A = 6*d₁ + 9*C_x = 0

Check the signs in the above equation. (Maybe just a typo.)

I tried using similar triangles:

The vertical side of the green triangle is not tangent to the right side of the pipe. So, I don't think that the horizontal side of the green triangle is 5 ft.

Maybe you can use the red triangle shown in the attachment to find the distance between D and C.

[EDIT: Oops. I see Simon posted while I was busy constructing my post.]

 

[haruspex]

I tried using similar triangles:

Judging from your sketch, you seem to have assumed that a vertical line tangential to the RHS of the pipe and a horizontal line tangential to the underside of the pipe will intersect CDE at the same point. That is not the case.

 

[pgardn]

The Attempt at a Solution

I isolated each part of the system:

.

Just curious as how the vertical bar will remain static if there are no force vectors down?

 

[TSny]

Just curious as how the vertical bar will remain static if there are no force vectors down?

Right, there must be a downward force. But it's ok to set it up as in the free body diagram. In working out the equations, you will just find that C_y is negative which indicates it's actually downward on the vertical rod and upward on the other rod.

 

[pgardn]

Right, there must be a downward force. But it's ok to set it up as in the free body diagram. In working out the equations, you will just find that C_y is negative which indicates it's actually downward on the vertical rod and upward on the other rod.

Yes.

Directions are pretty important for the diagonal rod in setting up your equations because as drawn you have 3 vertical forces or components of those forces. As drawn, the force labeled Ey will come out too large if one decided to start there.

 

[yaro99]

Thanks everyone for the help, I figured it out.
Using the triangle method suggested, with triangles BCP and PCD, I found that angle BCP = angle PCD = 1/2 angle BCD = (1/2)*arctan(8/6) = 26.6°

using the law of sines for BCP:
1.5/sin(26.6) = b/sin(63.4)
b = 3ft

and for PCD:
1.5/sin(26.6) = d/sin(63.4)
d = 3ft

where
d=|CD| and b=|CB|


this makes d₁ = 9 - 3 = 6ft, and d₂ = 10 - 3 = 7ft
Plugging these into my equilibrium equations (and fixing my error in the ƩM_A equation) I get the correct answers.

To find E_x and E_y I just used ƩF_x=0 and ƩF_y=0 for member CDE.

 

[yaro99]

Yes.

Directions are pretty important for the diagonal rod in setting up your equations because as drawn you have 3 vertical forces or components of those forces. As drawn, the force labeled Ey will come out too large if one decided to start there.

I'm not sure what you mean here, but I believe TSny is right in saying that it shouldn't matter. They are just assumed directions. If my answer comes out negative, the direction will be opposite of what it is on the diagram.

 

[pgardn]

I'm not sure what you mean here, but I believe TSny is right in saying that it shouldn't matter. They are just assumed directions. If my answer comes out negative, the direction will be opposite of what it is on the diagram.

I did the problem and made a math error. I then had two mistakes to correct because I also messed up on the direction of a force to begin with. Either way it did not work out so it resolved itself. Just took longer. I also should have started with the vertical bar using the knowns from the pipe.
Then again I drew similar triangles which eventually brought me right to the law of sines. So I did things the long way from the start.

For dynamics with a net torque it can become very troubling.

 

[yaro99]

I did the problem and made a math error. I then had two mistakes to correct because I also messed up on the direction of a force to begin with. Either way it did not work out so it resolved itself. Just took longer. I also should have started with the vertical bar using the knowns from the pipe.
Then again I drew similar triangles which eventually brought me right to the law of sines. So I did things the long way from the start.

For dynamics with a net torque it can become very troubling.

Ok thanks, good to keep in mind.