DBoy00
- 2
- 0
Homework Statement
I am in such a situation, where we are trying to measure the characteristics of a stepping motor in order to verify its operational characteristics.
I have tried measuring the motor's torque in many ways but I am having trouble following the company maker's method given. Perhaps my physics is not good enough, therefore I really want some help.
The question follows:
I am trying to measure pull-in and pull-out torque via analog simple pulley system.
The company showed us a demo on how they obtained their data. I do not fully understand the method.
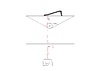
- The system comprises of the small stepper motor fixed in a V shaped suspension body by means of a rubber clamp
- The motor shaft is connected to a pulley or radius r
- A string fixed to the suspension body comes vertical down and wraps around the pulley twice before going towards the ground with a weight attached W
- The motor is then put under pull-in and pull-out measurements with varying weight
- Pull-in torque being operating the motor from rest with the weight attached, when a full rotation is not achieved after inputting a fixed number of steps, then it has slipped and reached it's limit
- Pull-out torque being accelerating the motor to the wanted speed then adding weigh till the motor stalls or slips
I only know the weight attached to the bottom of the string. I am pondering why the company would use such a method.
The data would be different depending on the string and the amount of times the string wraps around the pulley. Here's a picture to give the idea... I:m going to slap together in paint now. I have attached it since I cannot link without 15 posts... even though I attached it here
2. Homework Equations and questions
torque = F*length, W = mass*gravity, Ffriction = Fn*u
What would be the forces acting on the pulley surrounding the shaft? Would we not need the forced exerted on the point the string is attached to?
How does the tension in the rope relate to the normal force acting along the diameter of the pulley?
Basically how would I find the torque after knowing the weight at the end of the string.
The Attempt at a Solution
I have tried imagining the tension in the string acting evenly on all parts of the pulley... therefore if the pulley was flattened out then it would be a flat line with T acting on it. Since I wrapped it twice around the pulley, it'd be 2x the torque. However, after looking at it I think it is wrong. There is no way to guarantee that the T in the string would be acting on the pulley evenly. Furthermore T cannot be estimated as T, and Fn on the pulley therefore cannot be just T.
Another method I read in a book suggests that I take the torque as:
torque = (F1 - W)(r + a),
'a' being the rope thickness, 'F1' being the force from the rope above the pulley and 'W' being the weight of the load at the end of the string.