- #1
upender singh
- 14
- 0
1:question
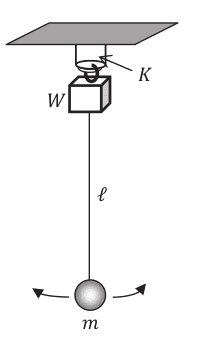
A weight W is suspended from a rigid support by a hard spring with stiffness constant k . The spring is enclosed in a hard plastic sleeve, which prevents horizontal motion, but allows vertical oscillations. A simple pendulum of length l with a bob of
mass m (mg<<W) is suspended from the weight W and is set oscillating in a horizontal line with a small amplitude. After some time has passed, the weight W is observed to be oscillating up and down with a large amplitude (but not hitting the sleeve). It follows that the stiffness constant k must be:
2:relevant equations
w^2=k/m
3:attempt
Please hint me where to start. I tried balancing the forces but that brought me nowhere.
A weight W is suspended from a rigid support by a hard spring with stiffness constant k . The spring is enclosed in a hard plastic sleeve, which prevents horizontal motion, but allows vertical oscillations. A simple pendulum of length l with a bob of
mass m (mg<<W) is suspended from the weight W and is set oscillating in a horizontal line with a small amplitude. After some time has passed, the weight W is observed to be oscillating up and down with a large amplitude (but not hitting the sleeve). It follows that the stiffness constant k must be:
- k=4w/l
- k=2w/l
- k=w/l
- k=w/2l
2:relevant equations
w^2=k/m
3:attempt
Please hint me where to start. I tried balancing the forces but that brought me nowhere.
Last edited: