Strange Change of Variable of Integration

[Recipi]

I've been following a few derivations for quantities in classical mechanics of rotating systems, and one of the integrals is transformed in a way I've never seen before. For angle theta, angular velocity omega and angular acceleration alpha:

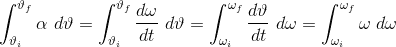
Intuitively I can see that they've 'just' swapped the differential on top with the one trailing the integral and adapted the variables denoting the initial and final values accordingly, but could anybody point me to a more in-depth explanation of this? The notes gloss over the step and it seems like it could be a useful trick to bear in mind generally.

 

[arildno]

Note that, between 2 and 3, you may write:
d\theta=\frac{d\theta}{dt}dt=\omega{dt}
You then make the variable change:
\frac{d\omega}{dt}dt=d\omega

 

[brmath]

Whenever you see people using change of variable (in integrals), or separating variables (in diff eq) and/or messing around with differentials in any way, it is always a shortcut way of applying the chain rule. You have the further slight complication here re the connections between $\alpha, \omega \text{ and } \theta$. Or perhaps it is an opportunity rather than a complication.

What Arildno wrote should show you the path.