riseofphoenix
- 294
- 2
7. The figure shows the path of a portion of a ray of light as it passes through three different materials. What can be concluded concerning the refractive indices of these three materials.
(A) n1 < n2 < n3
(B) n1 > n2 > n3
(C) n3 < n1 < n2
(D) n2 = n1 > n3
(E) n1 = n2 < n3
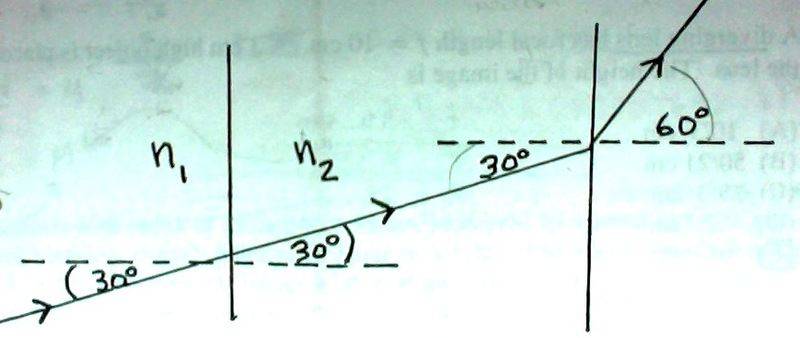
The answer is D...but WHY?!
According the the diagram above, n1 DOES in fact = n2. The ray of light just goes through each medium without bending or refracting. HOWEVER, once it hits the 3rd material, it bends!
And the angles for n1 and n2 (which are the same) are MUCH smaller than the angle for n3.
I chose E but that's the wrong answer. the Answer is D... why? :(
Does index of refraction refer to the angle of which the light is passing through each material??
I have a physics exam on wednesday and I'm stressed out because I also have a microbiology exam on that same day.
So i have to understand all the answers to the questions I missed on the previous tests to study for this exam
(A) n1 < n2 < n3
(B) n1 > n2 > n3
(C) n3 < n1 < n2
(D) n2 = n1 > n3
(E) n1 = n2 < n3
The answer is D...but WHY?!
According the the diagram above, n1 DOES in fact = n2. The ray of light just goes through each medium without bending or refracting. HOWEVER, once it hits the 3rd material, it bends!
And the angles for n1 and n2 (which are the same) are MUCH smaller than the angle for n3.
I chose E but that's the wrong answer. the Answer is D... why? :(
Does index of refraction refer to the angle of which the light is passing through each material??
I have a physics exam on wednesday and I'm stressed out because I also have a microbiology exam on that same day.
So i have to understand all the answers to the questions I missed on the previous tests to study for this exam