Stresses with thickwalled tube theory

[ladil123]

Hello


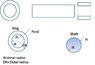
A ring should be mounted on a solid shaft. The rings inner diameter is smaller than than the shaft diamater so it will be forced on.
for my problem the inner diamater for the ring is 90mm -50 $$\mu$$m
the shaft is 90mm + 20$$\mu$$m

so there can be a difference of 110 $$\mu$$m.
This should give a certain stress after mounting the ring.

That stress is what I need to calculate

Im using thickwalled tube theory. plane strain.
I have attached a figure to make it easier...

If the radial stress in the ring starts with
S_radial=A - B/r^2
A, B are constants as we know.

with BC:
S_radial(r=OR)=0
S_radial(r=IR)= -Pi

so A=B/(OR^2)

and at the inner radius the stress is equal to the inner pressure: -Pi
So A=-Pi/(1/OR^2 -1/IR^2)/)

So the radial stress for the ring is :
SigmaRing=[-Pi/(1/OR^2 -1/IR^2)]/OR^2 + [Pi/(1/OR^2 -1/IR^2)]*1/r^2

If I do equlibrium for the solid shaft:
Witch BC:
Sigmaradial(r=0)=0
and Sigmaradial(r=IR)= -Pi

The constants A=0 and B=Pi*(IR^2)
So that stress is Sigmar=-Pi(IR^2)/r^2

What should I do to introduce the radial mismatch of 110 micro meters?
And after that how do I get the stress in the ring with my material data below ?

E-modulus ring =540 GPa
Poissons ring = 0.24
E-modulus shaft=205 GPa
Poissons shaft = 0.3


Thanks for any help

 

[nvn]

ladil123: For an answer to this question, see my post in thread 289475.