Engineering Struggling with a Structural Analysis Problem?

[howslifebrah]

Homework Statement

Hello everyone,

I am currently studying for an Mech Eng. Master's Program Entrance exam and am reviewing past test problems from the University website.

Problem statement:

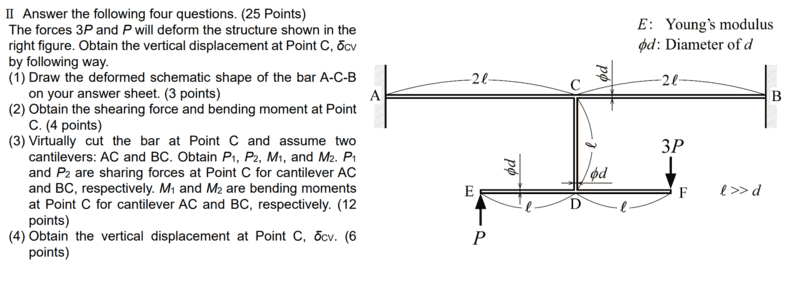
Answer the following four questions (45 min limit):

(1) Draw the deformed schematic shape of the bar A-C-B on your answer sheet. (3 points)
(2) Obtain the shearing force and bending moment at Point C. (4 points)
(3) Virtually cut the bar at Point C and assume two cantilevers: AC and BC. Obtain P1, P2, M1, and M2. P1 and P2 are sharing forces at Point C for cantilever AC and BC, respectively. M1 and M2 are bending moments at Point C for cantilever AC and BC, respectively. (12 points)
(4) Obtain the vertical displacement at Point C, δCV. (6 points)

I am currently stuck on part 3.

Relevant Equations

I am not allowed any reference material during the exam. This question seems very similar to the process of Slope-Deflection method for indeterminate frames so I believe it may be related.

Diagram of the problem below. I have 45 minutes to finish all parts of this question without reference material.

The Mechanics of Materials section of these tests are largely Structural Analysis, which I was not taught to this level in my undergrad degree so I am teaching myself via Youtube lectures. I think I must be lacking some critical information to solve some of the problems and I have no guidance so I am hoping for a push in the right direction here.

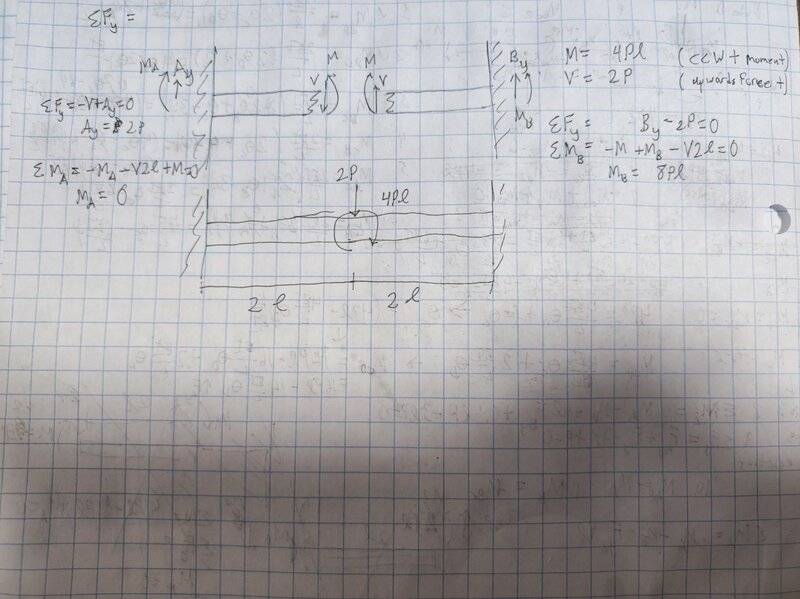
My first attempt at this problem has involved simplifying the I frame into a double fixed-end beam of length 4L with a CCW moment of 4PL and a downwards point load of 2P centered at 2L (shown below). However making virtual cantilevers from this point and using force and moment equilibrium equations has only been confusing when I tried to work it out. My attempt is not even remotely obeying equilibrium so please ignore it.

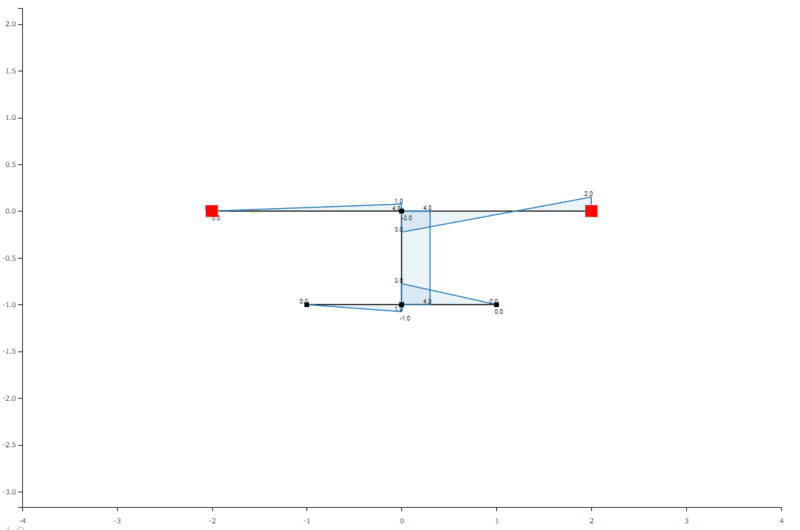
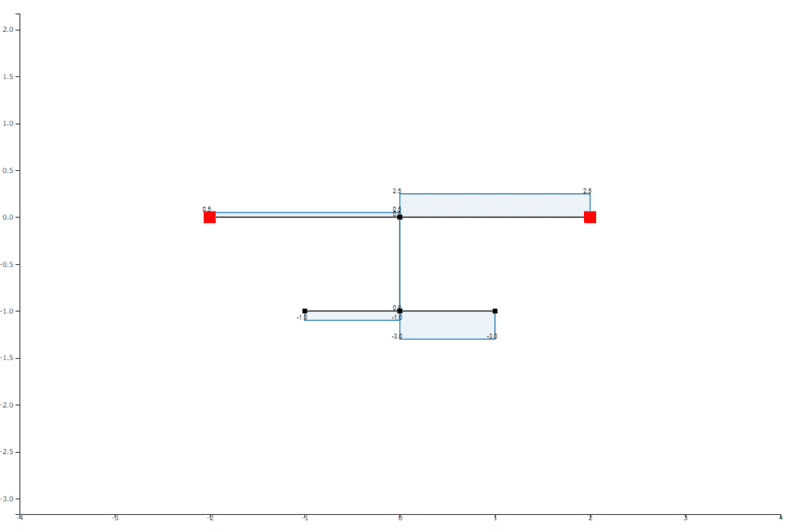
I then verified what the answer should be using the results of 2 frame calculators.

I was able to arrive at the same result as the calculator by using force method but that method is *considerably* too cumbersome to use given the test time and not what is being asked by the problem statement.

My gut feeling for a next step is that this can be solved by using slope deflection method. I assumed this is a sway frame with vertical displacement occurring at joint C. However, when I apply that method I run into a contradiction between my slope deflection equations for CA and CB and my moment equilibrium equation at joint C.

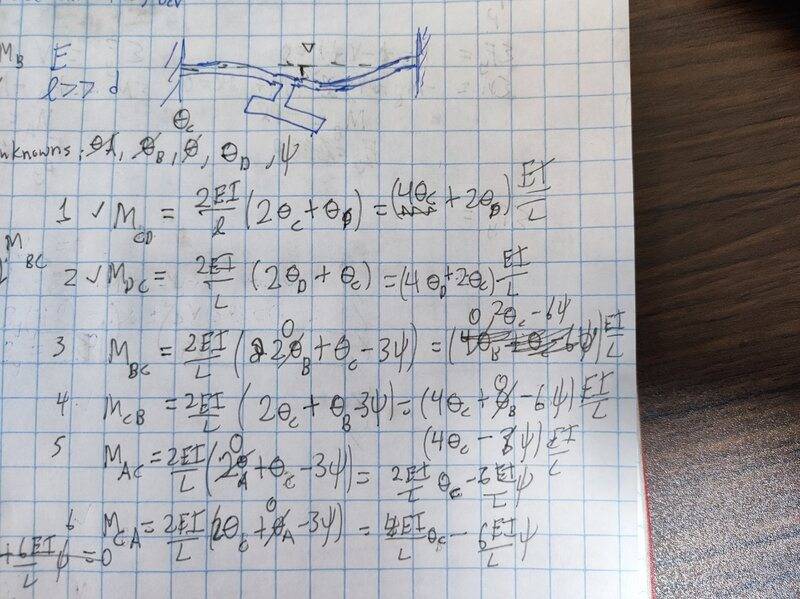
Equilibrium equations derived below:

MCB-MCA-MCD=0

However since there is no external loading on members AC and BC, my slope deflection equations for MCB and MCA perfectly cancel each other while MCD= 4PL. At this point I've exhausted my ideas. I'm hoping someone here can get me on track. Thanks!

 

[member38644]

It sounds like you are on the right track by considering the slope deflection method. However, it is important to note that this method can only be used for statically determinate structures. If the structure is statically indeterminate, then you will need to use other methods such as the moment distribution method or the stiffness method.

In order to determine if the structure is statically determinate or indeterminate, you can use the equation: 3n = 2j + r, where n is the number of members, j is the number of joints, and r is the number of support reactions. If this equation is satisfied, then the structure is statically determinate and can be solved using the slope deflection method.

If the structure is statically indeterminate, then you will need to use other methods such as the moment distribution method or the stiffness method. These methods can be more cumbersome, but they are necessary for solving indeterminate structures.

It is also important to make sure that your assumptions and simplifications are correct before attempting to solve the problem. Double check your diagram and make sure it accurately represents the given information. If you are still struggling, it may be helpful to seek guidance from a professor or tutor who is knowledgeable in structural analysis. Keep practicing and don't give up, you will get the hang of it eventually. Good luck!