scrilla103
- 2
- 0
Homework Statement
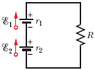
ε[1]=12v
internal resistance[1]=.016Ω
ε[2]=12v
internal resistance[2]=.012Ω
some unknown resistance 'R' in a stand alone resistor.
a) what value of 'R' will make the terminal-to-terminal potential difference of one of the batteries zero?
b) which battery would it be?
(picture below shows circuit)
Homework Equations
R = V/i
The Attempt at a Solution
I put together this equation:
ε[2] - ir[2] + ε - ir[1] - iR = 0
and continued to simplify to this:
i(.028 + R) = 24
The problem is I don't have a way to find 'i'...
Any ideas? This problem is marked as a three dot (harder difficulty) in my book, so I'm guessing there's an assumption I'm missing.
Thanks in advance,
Caleb