Study of harmonic motion of a liquid in a V shaped tube

[sumatoken]

Homework Statement

Study of harmonic motion of a liquid in a V shaped tube using the Lagrangian method.

Relevant Equations

What is the total potential energy of the system? and why is the restoring force considered to be only the one due to hydrostatic pressure?

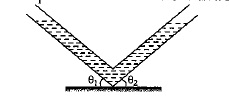
A V-shaped tube with a cross-section A contains a perfect liquid with mass density

and length L plus

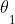and

the angles between the horizontal plane and the tube arms as shown in the attached figure.

We displace the liquid from its equilibrium position with a distance

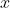and without any initial velocity.

I'm interested in applying the Lagrangian method.

For that, I need to determine both the system's kinetic energy and potential energy.

Kinetic energy is by definition:

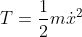
As for potential energy I need to know which forces to consider.

I can see three forces applied to the liquid:

- The force due to gravity

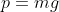with a potential energy

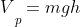
- The normal force due to the tube reaction. This force will have a null work therefore no potential energy.

- The force due to hydrostatic pressure on the liquid by the portion displaced of length

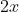with potential energy written in terms of the angles, cross-section A and

.

I did some research, and some solutions did not consider the potential energy due to gravity and considered the restoring force to be only the one due to hydrostatic pressure which I do not understand why.

Please feel free to correct me.

Mohammed

 

[Orodruin]

You should not consider forces at all in the Lagrange formalism. What you should be considering is the total potential energy, which here is solely due to gravity. Any pressure forces are internal to the fluid (or orthogonal to the motion) and therefore do not affect the potential.

 

[haruspex]

some solutions did not consider the potential energy due to gravity and considered the restoring force to be only the one due to hydrostatic pressure

Since it is gravity that leads to hydrostatic pressure, maybe considering both would be double counting.