How Does an Underwater Current Affect Submarine Navigation?

[andkand97]

Homework Statement

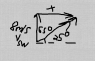
driving his homemade submarine underwater in a nearby lake. His instruments tell him that the sub is traveling at 8 m/s relative to the surrounding water and that the sub is oriented due north (nose pointing north). After two minutes, however, he ends up crashing into a sunken pirate ship. He is confused because he knows from his sonar that the pirate ship is located at a position 25° E of N, 600 m from his original position. The only explanation, he reasons, is that an underwater current must have caused him to drift off course. Calculate the speed and direction of the underwater current.

Homework Equations

I'm assuming I need to find acceleration so I used X=V_it+.5at²

The Attempt at a Solution

I got -0.05m/s² which I'm pretty sure is wrong.

 

[BvU]

Yes, a speed has a different dimension than m/s², so no surprise...

But, in order to help you a little: at t=0 he is traveling at 8 m/s wrt the water. And you may assume that stays constant. Where would he have ended up if he had a headwindwater of, say 2 m/s ?

Make a drawing

 

[andkand97]

So I do not need acceleration?

 

[BiGyElLoWhAt]

I don't think you need acceleration for this. It depends on how he's measuring his speed. I'm assuming he's just measuring how fast his prop is turning or something like that. If that's the case, the submarine is trying to go straight forward, but he ends up moving 25$^o$ offcourse.

So I guess this question (at least in my eyes) boils down to this: does he move with constant velocity to the ship or does he gradually accelerate towards the ship (implying he only measured his velocity at time t=0, and didn't look at it again until he crashed). Both are solveable, but you need to know which is the case first.

 

[SteamKing]

So I do not need acceleration?

There's nothing in the problem statement which indicates the submarine is accelerating.

If a vessel or a plane is caught in a current of some sort, the position of the plane or vessel will be shifted, relative to some fixed point, by the velocity and direction of the current relative to the velocity and direction of travel of the plane or vessel. The amount by which position shifts is proportional to the current velocity and the time spent in the current.

 

[BiGyElLoWhAt]

Well I think you answered my question steam.

 

[BvU]

Sub travels 600 m in 2 min, so his speed wrt the ground is ... with a direction ...
Sub speed wrt the water is 8 m/s north
What is the difference ? What makes the difference ? Voila !

 

[andkand97]

I'm sorry but I'm still a bit confused. Can someone break the problem down for me?

 

[andkand97]

Okay well I tried again and got a speed of 17.16m/s 65° N of E. Am I right?

 

[BiGyElLoWhAt]

Ok so the sub captain, let's call him Paul. Paul's cruising in his submarine, and he has this nifty thing attached to his prop (the spinning blade) which measure's his speed. It does some calculations and gives his speed based on how much water's leaving the prop, how fast it's spinning, etc. It say's he's moving 8m/s. Now it's very important for Paul to no only know how fast he's going, but the direction as well. Paul, naively, assumes that the direction that his sub is pointing is the direction he's travelling. Because of this, he crashes into a pirate ship that he knew was there, but didn't think he was headed towards. He's not actually moving straight forward. He's moving sideways (otherwise he wouldn't have crashed, right?).

What is his velocity?

 

[BiGyElLoWhAt]

Okay well I tried again and got a speed of 17.16m/s 65° N of E. Am I right?

Try showing your steps.

 

[andkand97]

Well what I did was I drew a picture (below; sorry it's sloppy). I found the angle was 65° so I took the cosine of 65=8/hypotenuse and that came out to be 18.93. So then I used that to find X. I did sin65=x/18.93 and got 17.16m/s. I think I may have the angle wrong though.

 

[BiGyElLoWhAt]

well 65 degrees is the correct direction for the resultant vector, but you're not trying to solve for the resultant vector. Ahh, after looking at your picture you do have the angle wrong. You didn't draw 25 degrees east of north, you drew 25 degress North of east.

 

[andkand97]

Ahhhh..So that would mean to find the velocity of the current I'd have to take tan25°=x/8 which would get me 3.73 m/s. But I still don't understand how to get the direction. Wouldn't the current be directly east?
Also I'm sorry for taking up your time. I think I'm complicating this a lot more than I need to.

 

[BiGyElLoWhAt]

Do you know about vectors and adding and subtracting them and stuff? It actually turns into a way simpler problem if you express his velocity as vector components. I'm taking for granted that you know Paul's actual velocity is the sum of the "velocity" from the submarine and the "velocity" of the current.
Break down all the vectors into components $<x,y>$ or $x \hat{i} + y \hat{j}$

$<x,y>_{submarine} + <a,b>_{current} = <u,v>_{actual}$
You are essentially "given 2 of these. See if you can figure out which 2 you have and what they are. After that it's just a simple equation to solve.

 

[andkand97]

I'm given the submarine and actual. The submarine is 8 m/s. The actual would be the 600 m in two minutes. Am I supposed to find the velocity from that? (600 m in two minutes) then put it into the equation you gave to solve for the current.

 

[BiGyElLoWhAt]

You need the vector form of that velocity, but yes.

 

[BiGyElLoWhAt]

And that equation that I gave isn't anything special, it just represents the information given and how it's related.

 

[Chestermiller]

Let v_x represent the component of the current velocity in the direction to the East, and v_y represent the component of the current velocity in the direction to the North. Similarly, let V_x and V_y represent the velocity components of the sub relative to the ground. Express V_x and V_y in terms of v_x and v_y. In terms of in terms of v_x and v<sub>y[/SUB, how far does the sub travel relative to the ground in time t?

Chet</sub>