Sum of Angle A and B: Does Proportion Matter?

  • Thread starter Thread starter Miike012
  • Start date Start date
  • Tags Tags
    Angle Matter Sum
AI Thread Summary
The discussion revolves around the proof involving the sum of angles A and B, particularly in the context of triangles and their leg proportions. The confusion arises from substituting one triangle for another despite differing leg ratios, questioning whether this affects the validity of the proof. Participants clarify that the triangles' similarity allows for such substitutions without altering the result, as they essentially multiply by a factor of one. The conversation also touches on the necessity of including a right triangle in the diagram to accurately represent the sine function. Ultimately, the proof demonstrates that angle relationships hold true regardless of the triangle sizes involved.
Miike012
Messages
1,009
Reaction score
0
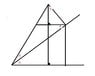
Ok.. I've been looking at the sum of angle A and angle B...
in the proof they substituted angle A ( adjacent to angle B ) for the upper right angle A.
It seems obvious that one can do this because they are the same exact angle, but what is confusing me is that the triangles do not have the same exact leg proportions... Does that not matter?
 

Attachments

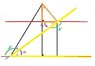
  • MATH.jpg
    MATH.jpg
    13.8 KB · Views: 439
Physics news on Phys.org
It has to do with the geometric proof of a line intersecting two parallels. Notice that the central line in the middle shows two right angles, so you know they are parallel.

More specifically:

zn8wfp.jpg


Hope that is what you were asking? It was a bit unclear.
 
Last edited:
I totally understand how they got the angles however I don't understand how they could exchange the triangle that I highlited in yellow for the triangle that I highlighted in orange... because after all when we use sine.. cos... tan... ect.. we are trying to find the leg ratios of a triangle... but if we use the smaller triangle that I highlited in orange.. it won't have the same ratio as the one in yellow..
The only way that I understand how they can use it is because it looks like they are multiplying by a factor of one.. so it wouldn't change the result...
 
I don't see any of the triangles highlighted? Could you re-upload the picture perhaps.
 
sorry... here it is..
 

Attachments

  • MATH.jpg
    MATH.jpg
    20.1 KB · Views: 442
I see what you are trying to do. Is this the proof for sin(a+b) ? If so, then your diagram is missing a right triangle. The hyp of both yellow and orange triangles should be perpendicular (because the hyp of the orange triangle is supposed to represent the sine of angle B). Knowing that, we can determine that the bottom right angle of the orange triangle is equal to (90-a). The top angle a is unknown for now, we will call it x. The remaining angle is 90. The sum of all three angles must be 180, so we can write an equation such as:

90 + x + (90-a) = 180
180 + x - a = 180
x - a = 180 - 180
x - a = 0

In order for x-a to equal zero, x must be a.
 

Thread 'Family of lines that are at a distance of 5 from the origin'

I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached. The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter. From my side, the only thing I could...
View full post »

Thread 'Making the denominator of a certain fraction real'

Essentially I just have this problem that I'm stuck on, on a sheet about complex numbers: Show that, for ##|r|<1,## $$1+r\cos(x)+r^2\cos(2x)+r^3\cos(3x)...=\frac{1-r\cos(x)}{1-2r\cos(x)+r^2}$$ My first thought was to express it as a geometric series, where the real part of the sum of the series would be the series you see above: $$1+re^{ix}+r^2e^{2ix}+r^3e^{3ix}...$$ The sum of this series is just: $$\frac{(re^{ix})^n-1}{re^{ix} - 1}$$ I'm having some trouble trying to figure out what to...
View full post »

Similar threads

Finding area of a non right angled triangle
Replies
9
Views
3K
Why does the dot product in this solution equal zero?
Replies
3
Views
1K
Proof of the trig identities for half-angles
Replies
1
Views
1K
Angles inscribed in circles part 1
Replies
6
Views
2K
Sum of the angles of a spherical triangle
Replies
1
Views
4K
Multiple angles : Reducing the sum
Replies
11
Views
2K
B A Question Relating Sum of Angles and Breaking of the Parallel Postulate
Replies
6
Views
1K
Why is this result different? (calculating the sides of a triangle)
Replies
6
Views
1K
Using the Law of Sines - Getting a Domain Error on my Calculator
Replies
8
Views
6K
Circle Problem: Solve an angle
Replies
22
Views
4K

Hot Threads

Recent Insights

Back
Top