Surface charge on a conductor due to a charged rod 'q'

[iVenky]

Homework Statement

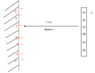
A charged rod of charge 'q' is at a distance 'd' from a perfect conductor as shown below.
What's the total surface charge on the conductor?

2. Homework Equations
I tried to solve this without equations.

The Attempt at a Solution

[/B]
Basically, as long as there is E field due to +q, it can draw a negative charge from the conductor to the surface. This would stop once the total E field on a point charge at infinity goes to 0. This should happen when the total charge on the surface is exactly -q. Is this explanation correct?

However, what's bothering me is the non-dependence on distance 'd'. If d-> ∞, then I wouldn't expect 'q' draw any charge on the conductor since E field would be zero at d-> ∞. Then what's wrong here?
Also, does this explanation work even if this conductor is not perfect (has a σ≠∞)

 

[Orodruin]

If d-> ∞, then I wouldn't expect 'q' draw any charge on the conductor since E field would be zero at d-> ∞. Then what's wrong here?

The charge density becomes lower as the induced charge will be spread over a larger portion of the conductor.

Also, does this explanation work even if this conductor is not perfect (has a σ≠∞)

The problem only deals with the static situation, i.e., the situation after a long time has passed. With finite conductance that will take longer to achieve for a non-perfect conductor, but the end result would be the same.