Suspended Block: Find Tensions T1 & T2

[Dan350]

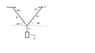
1. A block of mas M=17kg is suspended by three ropes as shown in the figure. The two ropes attached to the ceiling each make an angle of 41° with the horizontal

a)What is the tension T2 in the vertical rope?
b)What is the tension 1 in the ropes attached to the ceiling?

Homework Equations

F=ma3.
I made up these formulas:
Fx=T2cosθ2-T1cosθ1=0
Fy=T1sinθ1+T2sinθ2+T3=mg or Fy=T1sinθ1+T2sinθ2+T3-mg= 0

My idea is to rewrite T2 in terms of T1 in the Fx ecuation so then i would substitue to get the value of T2
I had made a similar problem like this, and using this procedure. but the difference is that Tension 3, how does it affect the problem? it does no affect the Fx forces,, but it does for the Fy, right?
With this i would get T2

Would you explain to me?
THanks!

The image is above

 

[Dan350]

Please make that angle 41,, the one of the image is 44 thanks

 

[voko]

The Fy equation cannot be correct. If it has T1 & T2, it cannot have mg, because mg applies to the block, and the only other force acting on the block is T3.