DUET
- 55
- 0
Hello!
The following system of linear equations
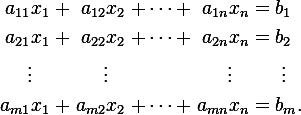
has been expressed in term of column vector in the following.
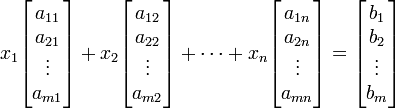 .
.
How can I express the system of linear equations in term of row vector?
In addition, What is the field of scalars? I would request to explain it.
Thanks in advance.
The following system of linear equations
has been expressed in term of column vector in the following.
How can I express the system of linear equations in term of row vector?
In addition, What is the field of scalars? I would request to explain it.
Thanks in advance.
Last edited: