System of Masses and Pulley, Problem

[fsun]

Homework Statement

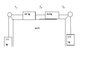
Calculate T1, T2 and T3. JPeg image of problem is attached.

Homework Equations

Sum of all forces = Mass of system x Acceleration of System

The Attempt at a Solution

I think I have T1 and T3 figured out but I am having problems with T2.
if the (E = sum of)
EF = ma
T2 + Ff = ma (Ff = 0 b/c u = 0)
however 0.5 kg is hanging so Fg is acting on T2
So i treated Fg of 0.5 kg mass like I would friction. The thing that is troubling me is that I thought you could only add up forces in the same plane. i.e. x-plane or y-plane.

a = 0.61 m/s^2 to the left, from previous work

How do I relate Fg from the 0.5 mass with T2 (going left?)

My first attempt:

T2:
EF = ma = T2 +Fg
(4.5 kg)(0.61m/s^2) = T2 + (0.5kg)(-9.8m/s^2)
T2 = 7.6 N

I had two issue. B/C everything is accelerating to the left, I thought a should equal -0.61m/s^2 but then the T2 value seems too small.

The second issue relates to Fg in the y-plane and T2 in the x-plane. Can you sum these forces up?

Should t1 > t2 > t3? or not?


Thanks

 

[ehild]

Gravity acts on every masses, but the gravitational force of one mass does not act on an other mass. Consider both blocks on the table separately. What forces act on the 2.5 kg block? Gravity of magnitude 2.5g acts downward, but it is canceled by the normal force from the table. Two pieces of string are connected to it. One piece pulls the block forward, the other piece pulls backwards. There are no more forces. The tension is the same in a string along all its length. So you know one force. And you know the acceleration: it is 0.61 m/s2 on the left. From this you can determine the resultant force exerted by the two strings.


ehild

 

[fsun]

My T2 solution above does not include direction for acceleration. However if I include the direction (left therefore "-" 0.61m/s^2) The tension seems to small. Under the assumption that T1 > T2 > T3.

 

[ehild]

At last I understood what you did. Your result T2=7.6 N is correct. And also T1>T2>T3.

The usual way to treat such problems is that we consider all bodies separately, but assume that all have the same acceleration. The direction of acceleration is along the string.

It is obvious to assume that the 1 kg mass will accelerate downward, under the effect of gravity and the tension T1 of the first string.

m₁ a=m₁g-T1

The second block of 2.5 kg mass is pulled to the left by the left string with force T1 and pulled to the right with the second string by force T2.

m₂ a=T1-T2

The third block is pulled forward by T2 and backwards by T3

m₃ a=T2-T3

The third block is pulled up by the third string with force T3 and gravity acts on it downward.

m₄ a=T3-m₄ g


Adding up all equations, the tensions cancel and we get that the sum of all external forces is equal to the acceleration times the sum of the masses, and this acceleration is 0.613 m/s².

Plugging that value for a in the first equation,

T1= 1kg (9,8-0.613)=9.187 N.

T2 is obtained from the second equation:

2.5 *0.613=9.19-T2---> T2=7.654 N

and T3 comes from the third or fourth one:

4*0.613=T2-T3 --->T3=5.202 N

The fourth equation:T3-0.5 g = 0.613*0.5 --->T3=5.206 N.

The difference in the last digit comes from rounding error.

ehild

 

[rwisz]

for your question! It seems like you are on the right track with your solution. Let's break it down step by step.

First, we can start by labeling all the forces acting on the system. We have T1, T2, T3, Fg (the weight of the 0.5 kg mass), and Ff (the friction force). We also know that the net force acting on the system is equal to the mass of the system (4.5 kg) times its acceleration (0.61 m/s^2). So we can write:

ΣF = ma = (4.5 kg)(0.61 m/s^2)

Next, we can look at the forces acting on each of the masses separately. For T1 and T3, the only other force acting on them is the weight of the 0.5 kg mass. So we can write:

T1 + Fg = (0.5 kg)(-9.8 m/s^2) (note that we use a negative sign for the weight because it is acting in the opposite direction of T1 and T3)

T3 + Fg = (0.5 kg)(-9.8 m/s^2)

Now for T2, we have two forces acting on it: T2 itself and the friction force Ff. So we can write:

T2 + Ff = ma = (4.5 kg)(0.61 m/s^2)

Now we can solve for each of the tensions:

T1 = (0.5 kg)(-9.8 m/s^2) - Fg = -4.9 N - Fg

T2 = (4.5 kg)(0.61 m/s^2) - Ff = 2.745 N - Ff

T3 = (0.5 kg)(-9.8 m/s^2) - Fg = -4.9 N - Fg

So now we just need to find the values of Ff and Fg. We can do this by using the equations for friction and weight:

Ff = μN = μmg (where μ is the coefficient of friction, and N is the normal force)

Fg = mg

We know that the coefficient of friction is 0, so Ff = 0. And we can calculate Fg:

Fg = (0.5 kg)(9.8 m