liljediboi
- 27
- 0
hey. i am in a physics honors class, and we just had a test.
each test has 9 questions, 8 which are decent, and the last one is the "death problem" this problem is worth 20 point, double of the others (if you did the math, if you get die on the death problem, the highest score possible is 80).
anyways. the last death problem is as follows
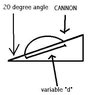
a cannon fires a projectile (no air or wind) at 100 m/s at a 20 degrees angle north of west. it is fired down a "hill" (which is impossibly straight) the hill has a 20 degree angle north of east. find d (see picture.
talked to tons of people, nobody knows if they got it, and many did not even have time to do it. looks like a huge curve coming.
and the obvious question. WHAT IS THE ANSWER?? and please show work for full credit. haha
each test has 9 questions, 8 which are decent, and the last one is the "death problem" this problem is worth 20 point, double of the others (if you did the math, if you get die on the death problem, the highest score possible is 80).
anyways. the last death problem is as follows
a cannon fires a projectile (no air or wind) at 100 m/s at a 20 degrees angle north of west. it is fired down a "hill" (which is impossibly straight) the hill has a 20 degree angle north of east. find d (see picture.
talked to tons of people, nobody knows if they got it, and many did not even have time to do it. looks like a huge curve coming.
and the obvious question. WHAT IS THE ANSWER?? and please show work for full credit. haha
Attachments
Last edited: