Take v(t) and h(t) to make v(h)

[Adoniram]

So I have some very complicated functions that do not have trivial inverses, but I'd really like to make a new function from them. What I have is:
v(t): velocity as a function of time
h(t): height as a function of time (never mind that is says hb)

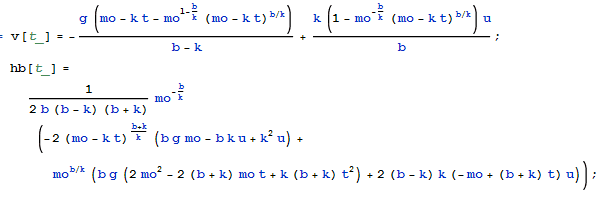
What I want:
v(h): velocity as a function of height

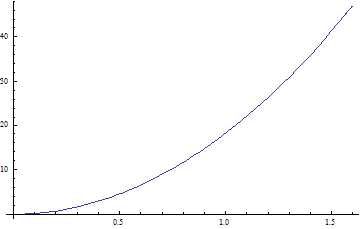
The height function goes as an exponential function, so there are no local minima to worry about:

Other than fitting a polynomial to the h(t) function (which I'm not sure would be invertible anyway), does anyone know of a good way to combine these functions into v(h)?

 

[FactChecker]

I don't know if there is a closed-form analytical solution, but since you are sure that h(t) is monotonically increasing, you could make a table of t as a function of h and fit a function through it.
From the looks of it, I would first try taking a logarithm of height and see if a regression line gives you the accuracy you want.
If that doesn't work, you can fit a spline function through it and make the resolution as good as you need. (A spline would only be practical if you make computer code to implement it.)

 

[mfb]

How/where do you need v(h)? It is easy to calculate individual points, and you can also calculate the derivative v'(h) analytically for every point where you know t.
If (b+k)/k is a small integer, it is possible to write down t(h) in closed form, otherwise it is probably impossible.

Introducing new variables for t-independent stuff would make the equations much more readable.

 

[Adoniram]

The reason I want this v(h) form is so that I can integrate a function which relies, in part, on v(t).

So... I have another function:
$$F(t,h)=c_1v(t)+c_2g(h)$$
where $c_1$ and $c_2$ are constants and $g(h)$ is another well-understood function of height.
What I want to find is:
$$\int_{h=0}^{h_f}F dh$$
to find the work done by this force over some height. And since velocity and height are well-defined functions, I figured it would make my life easier to integrate over a single variable, $dh$, instead of trying to figure out how to get work from a function of both time and height.

So, if I could get $t(h)$ and plug that into $v(t(h))$, my life would be easier...

Unfortunately, the quantity $(b+k)/k$ will be, at best, $1$ so it can't be ignored...

 

[Adoniram]

Ummm... maybe I could do this (please comment your thoughts!):

$$\int_{h=0}^{h_f} F dh = \int_{h=0}^{h_f} F dh \frac{dt}{dt} = \int_{t=0}^{t_f} F v(t) dt$$

Does that work, or is there a different conversion for the limits of integration or differential element that I'm forgetting?

 

[FactChecker]

Do you need it to be closed form or can you use numerical methods?

 

[Adoniram]

Do you need it to be closed form or can you use numerical methods?

Numerical results are perfectly fine!

 

[mfb]

Unfortunately, the quantity (b+k)/k will be, at best, 1 so it can't be ignored...

If it is 1, h(t) is a polynomial of degree 2, and easy to invert.

Numerically, you can just integrate over t and don't need anything special.

 

[Adoniram]

Yeah the problem is, it'll never be 1 in reality. It'll be something like (0.05+k)/k which is why it's so hard to invert.

 

[mfb]

All that doesn't matter if you just need a numerical value for the integral.