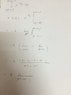Pual Black
- 91
- 1
Homework Statement
Hi sorry if the titel is wrong
I want to know if i can write this
##a^2 + u^2 -2au= (a-u)^2 = (u-a)^2##
I get different results when integrating ##x^{-\frac{3}{2}}## in the range ##(a-u)^2## to ##(a+u)^2##