What is Basis vectors: Definition and 76 Discussions

In mathematics, a set B of vectors in a vector space V is called a basis if every element of V may be written in a unique way as a finite linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to B. The elements of a basis are called basis vectors.
Equivalently, a set B is a basis if its elements are linearly independent and every element of V is a linear combination of elements of B. In other words, a basis is a linearly independent spanning set.
A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space.
This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces.

View More On Wikipedia.org
Recent contents Top users
  1. danielhaish

    B How addition of vectors works if every force is quantized

    Assuming two forces applied on an object in two vector one horizontal to the object and the other vertical, By vector addition the resulting vector would be in 45 degrees. (0,1) + (1,0) = (1,1) So the object acceleration direction would be as the following graph. But if the force that...
  2. D

    I Vector subspace and basis vectors in the context of data science

    The book I am studying from presents vector subspace as an infinite collection of vectors in a vector space with the properties of additive and multiplicative closure and basis vectors as a way to characterize/write a subspace compactly. All the vectors in the subspace can be written as linear...
  3. SH2372 General relativity (2X): Basis vectors in polar coordinates

    SH2372 General relativity (2X): Basis vectors in polar coordinates

    • Orodruin
    • Media item
    • Basis vectors Polar coordinates
    • Comments: 0
    • Category: Relativity
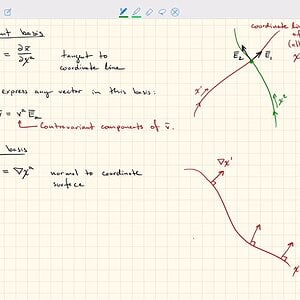
  4. SH2372 General Relativity (2): Tangent and dual bases

    SH2372 General Relativity (2): Tangent and dual bases

    • Orodruin
    • Media item
    • Basis vectors Tangent vector
    • Comments: 0
    • Category: Relativity
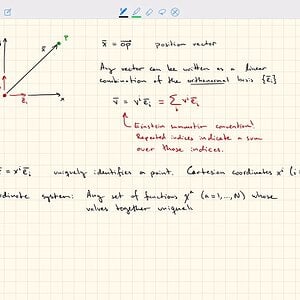
  5. SH2372 General Relativity (1): Euclidean space and coordinate systems

    SH2372 General Relativity (1): Euclidean space and coordinate systems

    • Orodruin
    • Media item
    • Basis vectors Coordinate systems Euclidean space
    • Comments: 0
    • Category: Relativity
  6. e2m2a

    I Confusion between vector components, basis vectors, and scalars

    There is an ambiguity for me about vector components and basis vectors. I think this is how to interpret it and clear it all up but I could be wrong. I understand a vector component is not a vector itself but a scalar. Yet, we break a vector into its "components" and then add them vectorially...
  7. K

    MHB Determine the area, calculate the basis vectors and determine the inner product

    A coordinate system with the coordinates s and t in R^2 is defined by the coordinate transformations: s = y/y_0 and t=y/y_0 - tan(x/x_0) , where x_0 and y_0 are constants. a) Determine the area that includes the point (x, y) = (0, 0) where the coordinate system is well defined. Express the...
  8. K

    Calculate the dual basis and tangent basis vectors

    a) Since ##tan(x/x_0)## is not defined for ##x=\pm\pi/2\cdot x_0## I assume x must be in between those values therefore ##-\pi/2\cdot x_0 < x < \pi/2\cdot x_0## and y can be any real number. Is this the correct answer on a)? b) I can solve x and y for s and t which gives me ##y=y_0\cdot s## and...
  9. Athenian

    Finding the Basis Vectors for a Coordinate System

    To my understanding, to get the basis vectors for a given coordinate system (in this case being the elliptic cylindrical coordinate system), I need to do something like shown below, right? $$\hat{\mu}_x = \hat{\mu} \cdot \hat{x}$$ $$\hat{v}_z = \hat{v} \cdot \hat{z}$$ And do that for...
  10. S

    B Relating basis vectors at different points in a neighborhood

    I'm reading a section on the derivative of a vector in a manifold. Quoting (the notation ##A^{\alpha}_{\beta'}## means ##\partial x^{\alpha}/\partial x^{\beta'}## - instead of using primed and unprimed variables, we use primed/unprimed indices to distinguish different bases): Now this "we know...
  11. George Keeling

    A Exploring Null Basis Vectors, Metric Signatures Near Kruskal

    On the way to Kruskal coordinates, Carroll introduces coordinates ##\left(v^\prime,u^\prime,\theta,\phi\right)## with metric equation$$ {ds}^2=-\frac{2{R_s}^3}{r}e^{-r / R_s}\left(dv^\prime du^\prime+du^\prime dv^\prime\right)+r^2{d\Omega}^2 $$ ##R_s=2GM## and we're using a ##-+++## signature...
  12. S

    I Tangent space basis vectors under a coordinate change

    I'm studying 'Core Principles of Special and General Relativity' by Luscombe - the chapter on tensors. Quoting: The book goes on to talk about a switch to the spherical coordinate system, in which ##\mathbf{r}## is specified as: $$\mathbf{r}=r\sin\theta\cos\phi\ \mathbf{\hat...
  13. Ishika_96_sparkles

    I Feynman's Lectures volume III (Ch:8) -- Resolution of vector states

    In the section 8-2 dealing with resolving the state vectors, we learn that |\phi \rangle =\sum_i C_i | i \rangle and the dual vector is defined as \langle \chi | =\sum_j D^*_j \langle j |Then, the an inner product is defined as \langle \chi | \phi \rangle =\sum_{ij} D^*_j C_i \langle j | i...
  14. R

    I The Levi-Civita Symbol and its Applications in Vector Operations

    Hello all, I was just introduced the Levi-Civita symbol and its utility in vector operations. The textbook I am following claims that, for basis vectors e_1, e_2, e_3 in an orthonormal coordinate system, the symbol can be used to represent the cross product as follows: e_i \times e_j =...
  15. Pencilvester

    I Lie derivative of hypersurface basis vectors along geodesic congruence

    Hello PF, here’s the setup: we have a geodesic congruence (not necessarily hypersurface orthogonal), and two sets of coordinates. One set, ##x^\alpha##, is just any arbitrary set of coordinates. The other set, ##(\tau,y^a)##, is defined such that ##\tau## labels each hypersurface (and...
  16. S

    I How do you derive those basis vectors in GR?

    You may be familiar with how you can express a vector field as a linear combination of basis vectors like so: X = Xi∂i Now, I know that normally, the basis vectors ∂i can be derived by taking the derivatives of the position vector for the coordinate system with respect to all the axes like...
  17. D

    I Deriving tensor transformation laws

    Hi, I'm worried I've got a grave misunderstanding. Also, throughout this post, a prime mark (') will indicate the transformed versions of my tensor, coordinates, etc. I'm going to define a tensor. $$T^\mu_\nu \partial_\mu \otimes dx^\nu$$ Now I'd like to investigate how the tensor transforms...
  18. M

    Prove that the standard basis vectors span R^2

    Homework Statement I know how to approach this problem; however, I'm just confused as to why we consider that R^2 is a vector space over the field R, and not Q or any other field for this question? Standard basis vectors: e_1, e_2 or i,j
  19. olgerm

    I How are basis vectors defined?

    hi. if I know how to convert coordinates from a system to cartesian system, then how can I find basevectors of that coordinatesystem? Is it possible that basevectors are different in different points(with different coordinates)? What is most general definition of basevectors? I tought it would...
  20. M

    Dot product and basis vectors in a Euclidean Space

    Homework Statement I am asked to write an expression for the length of a vector V in terms of its dot product in an arbitrary system in Euclidean space. Homework EquationsThe Attempt at a Solution The dot product of a vector a with itself can be given by I a I2. Does that expression only apply...
  21. M

    Derivative of basis vectors

    Homework Statement I am unsure as to how the partial derivative of the basis vector e_r with respect to theta is (1/r)e_theta in polar coordinates Homework EquationsThe Attempt at a Solution differentiating gives me -sin(theta)e_x+cos(theta)e_y however I'm not sure how to get 1/r.
  22. K

    I Basis Vectors & Inner Product: A No-Nonsense Introduction

    I read from this page https://properphysics.wordpress.com/2014/06/09/a-no-nonsense-introduction-to-special-relativity-part-6/ that the basis vectors are the canonical basis vectors in any coordinate system. This seems to be wrong, because if that was the case the metric would be the identity...
  23. N

    B Tensor Product, Basis Vectors and Tensor Components

    I am trying to figure how to get 1. from 2. and vice versa where the e's are bases for the vector space and θ's are bases for the dual vector space. 1. T = Tμνσρ(eμ ⊗ eν ⊗ θσ ⊗ θρ) 2. Tμνσρ = T(θμ,θν,eσ,eρ) My attempt is as follows: 2. into 1. gives T = T(θμ,θν,eσ,eρ)(eμ ⊗ eν ⊗ θσ ⊗ θρ)...
  24. P

    B Minkowski metric, scalar product, why the minus sign?

    In Schutz's A First Course in General Relativity (second edition, page 45, in the context of special relativity) he gives the scalar product of four basis vectors in a frame as follows: $$\vec{e}_{0}\cdot\vec{e}_{0}=-1,$$...
  25. nacreous

    Calculate coefficients of expansion for vector y

    Homework Statement Let v(0) = [0.5 0.5 0.5 0.5]T, v(1) = [0.5 0.5 -0.5 -0.5]T, v(2) = [0.5 -0.5 0.5 -0.5]T, and z = [-0.5 0.5 0.5 1.5]T. a) How many v(3) can we find to make {v(0), v(1), v(2), v(3)} a fully orthogonal basis? b) What are z's coefficients of expansion αk in the basis found in...
  26. C

    Linear Algebra - Finding coordinates of a set

    Homework Statement Find the coordinates of each member of set S relative to B. B = {1, cos(x), cos2(x), cos3(x), cos4(x), cos5(x)} S = {1, cos(x), cos(2x), cos(3x), cos(4x), cos(5x)} I am to do this using Mathematica software. Each spanning equation will need to be sampled at six separate...
  27. Zero2Infinity

    Basis of the intersection of two spaces

    Homework Statement Consider two vector spaces ##A=span\{(1,1,0),(0,2,0)\}## and ##B=\{(x,y,z)\in\mathbb{R}^3 s.t. x-y=0\}##. Find a basis of ##A\cap B##. I get the solution but I also inferred it without all the calculations. Is my reasoning correct Homework Equations linear dependence...
  28. Matejxx1

    Find the basis of a kernel and the dimension of the image

    Homework Statement Let ##n>1\in\, \mathbb{N}##. A map ##A:\mathbb{R}_{n}[x]\to\mathbb{R}_{n}[x]## is given with the rule ##(Ap)(x)=(x^n+1)p(1)+p^{'''}(x)## a)Proof that this map is linear b)Find some basis of the kernel b)Find the dimension of the image Homework Equations ##\mathbb{R}_{n}[x]##...
  29. Kevin McHugh

    I Wedge product of basis vectors

    Is there a set of relationships for the wedge product of basis vectors as there are for the dot product and the cross product? i.e. e1*e1 = 1 e1*e2 = 0 e1 x e2 = e3
  30. S

    I Original direction of force versus vector components

    What happens to a mechanical force's real original direction i.e. when we divide it into components of basis vectors, which in turn change as per problem at hand (like gravity components at inclined plane ), how we arrive at correct physics by taking two/three arbitrary directions of our choice...
  31. D

    How to find basis vectors for a+ ax^2+bx^4?

    I want to find basis for a+ax^2+bx^4 belong to p4. I am getting the following result is it right? =>a(1+x^2) + b(x^4) => basis ={1+x^2, x^4} Is that right ? Please help me any help is appreciated.
  32. M

    Covariant and contravariant basis vectors /Euclidean space

    I want ask another basic question related to this paper - http://www.tandfonline.com/doi/pdf/10.1080/16742834.2011.11446922 If I have basis vectors for a curvilinear coordinate system(Euclidean space) that are completely orthogonal to each other(basis vectors will change from point to point)...
  33. J

    Vector Analysis using Basis Vectors

    Hi pf, Having some trouble with basis vectors for expanding a given vector in 3-D space. Any given vector in 3-D space can be given by a sum of component vectors in the form: V = e1V1 + e2V2 + e3V3 (where e1, e2 and e3 are the same as i, j and k unit vectors). Equation 1. I am happy with...
  34. Z

    Are photons really anti-correlated off their basis vectors?

    The wiki page https://en.wikipedia.org/wiki/Bell's theorem states the following which I agree with: Suppose the two particles are perfectly anti-correlated—in the sense that whenever both measured in the same direction, one gets identically opposite outcomes, when both measured in opposite...
  35. askhetan

    Matrix Elements as images of basis vectors

    I'm trying to understand the maths of QM from Shankar's book - Principles of Quantum Mechanics: On page 21 of that book, there is a general derivation that if we have a relation: |v'> = Ω|v> Where Ω is a operator on |v> transfroming it into |v'>, then the matrix entries of the operator can be...
  36. sunrah

    Basis vectors of Minkowski space

    Hi, I'm doing a first course in GR and have just found out that \eta_{ab} = g(\vec{e}_{a}, \vec{e}_{b}) = \vec{e}_{a} \cdot \vec{e}_{b} where g is a tensor, here taking the basis vectors of the space as arguments. I haven't seen this written explicitly anywhere but does this mean that...
  37. D

    SR & Lorentz Scalar Fields: Covariant Diff. & Wave Amplitude

    Hi. In GR , covariant differentiation is used because the basis vectors are not constant. But , what about in SR ? If the basis vectors are not Cartesian then they are not constant. Does covariant differentiation exist in SR ? And are for example spherical polar basis vectors which are not...
  38. R

    How Many Basis Vectors in Hilbert Space?

    What is the dimensionality, N, of the Hilbert space (i.e., how many basis vectors does it need)? To be honest I am entirely lost on this question. I've heard of Hilbert space being both finite and infinite so I'm not sure as to a solid answer for this question. Does the Hilbert space need 4...
  39. S

    Figuring out Bravais lattice from primitive basis vectors

    Homework Statement Given that the primitive basis vectors of a lattice are ##\mathbf{a} = \frac{a}{2}(\mathbf{i}+\mathbf{j})##, ##\mathbf{b} = \frac{a}{2}(\mathbf{j}+\mathbf{k})##, ##\mathbf{c} = \frac{a}{2}(\mathbf{k}+\mathbf{i})##, where ##\mathbf{i}##, ##\mathbf{j}##, and ##\mathbf{k}## are...
  40. M

    Classifications of basis vectors

    Hello every one , in this pic i just printed ( Tensors_The Mathematics of Relativity Theory and Continuum Mechanics by Anadijiban Das ) here the author classifies the basis into 3 types 1- is the general basis (non-holomonic ) , 2- coordinate basis ( holomonic ),3- orthonormal basis ( non-...
  41. M

    A Bit Confused About Polar Basis Vectors

    Let me say from the beginning I'm not talking about the non-coordinate unit vectors for polar coordinates. I'm talking about basis vectors. Let me just ask it as boldly as possible: how does one use these basis vectors in order to describe a vector? I know they are different at every point, so...
  42. nomadreid

    Confusion about basis vectors and matrix tensor

    In "A Student's Guide to Vectors and Tensors" by Daniel Fleisch, I read that the covariant metric tensor gij=ei°ei (I'm leaving out the → s above the e's) where ei and ei are coordinate basis vectors and ° denotes the inner product, and similarly for the contravariant metric tensor using dual...
  43. E

    2-dimension polar basis vectors

    I'd like to understand why i cannot seem to be able to define unit polar basis vectors. Let me explain: We have our usual polar coordinates relation to Cartesian: x = r cosθ ; y = r sinθ if I define \hat{e_{r}}, \hat{e_{\vartheta}} as the polar basis vectors, then they should be...
  44. B

    Multiplying matrix units and standard basis vectors

    Hello all, I don't have a question on homework specifically, but I need clarification on something I'm reading in the textbook. I will be starting an abstract algebra class in the spring and it's been quite a few years since I've had linear algebra, so I'll be reviewing that material before the...
  45. H

    Coordinate and dual basis vectors and metric tensor

    I have been reading an introductory book to General Relativity by H Hobson. I have been following it step by step and now I am stuck. It is stated in the book that: "It is straightforward to show that the coordinate and dual basis vectors themselves are related... "ea = gabeb ..." I have...
  46. S

    Basis vectors definition

    Homework Statement A vector is a geometrical object which doesn't depend on the basis we use to represent it, only its components will change. We can express this by \vec{A}=ƩA_i \hat{ε_i} = Ʃ\tilde{A_i} \vec{ε_i}, where it has been emphasized that the basis ε is not necessarily orthonormal...
  47. R

    What's the difference between lattice vectors and basis vectors?

    Google has not been very useful, and Kittel has too little on crystallography. Actually, what's a good source on crystallography?
  48. V

    Orthonormal basis vectors for polar coordinate system

    Firstly; is there a difference between the "regular" polar coordinates that use \theta and r to describe a point (the one where the point (\sqrt{2}, \frac{\pi}{4}) equals (1, 1) in rectangular coordinates) and the ones that use the orthonormal basis vectors \hat{e}_r and...
  49. B

    Completeness of a set of basis vectors in 3D Euclidean space.

    Homework Statement The problem is Exercise 2 in the picture http://postimage.org/image/3ou3x1sh7/ Homework Equations The hint says: can you express and three-dimensional vector in terms of just two linearly independent vectors? The Attempt at a Solution I have no idea where...
  50. H

    Understanding Basis Vectors and One-Forms: A Simplified Explanation

    Greetings, I have just started studying manifolds, and have come across the idea that the basis vectors can be expressed as: e\mu = \partial/\partialx\mu. I tried to convince myself of this in 2D Cartesian coordinates using a pretty non-rigorous derivation (the idea being to get a...
Back
Top