jones123
- 10
- 0
Hi,
From the first law of thermodynamics it follows:
Cp * (δT/δt) = (δQ/δt)
where Cp = specific heat capacity, T = temperature, Q = heat, t = time
From this formula, you would derive that temperature keeps on increasing as long as dQ/dt > 0. But if you, for example, look at the idealized diurnal evolution of air temperature, it can be seen that the temperature keeps on increasing until its maximum value, despite the fact that there is net heat loss (dQ/dt < 0 for example between noon and 4h where the area between both curves becomes smaller)...
It seems that on the figure here the temperature keeps on rising as long as the value of Q itself > 0 but that doesn't necessarily mean that dQ/dt has to be > 0, right? Is my reasoning wrong or how can this correctly be explained with formulas?
Thanks already!
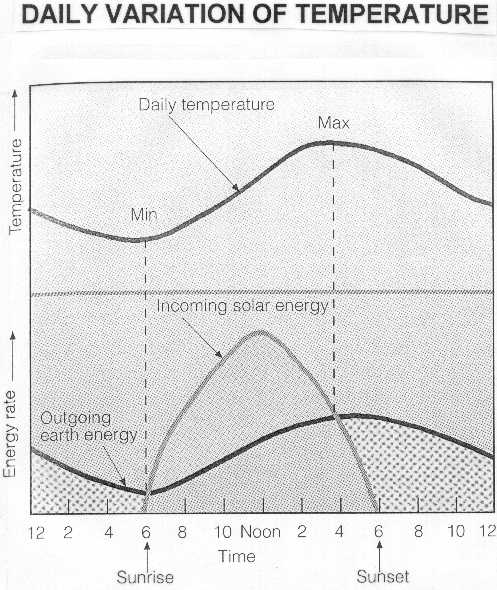
From the first law of thermodynamics it follows:
Cp * (δT/δt) = (δQ/δt)
where Cp = specific heat capacity, T = temperature, Q = heat, t = time
From this formula, you would derive that temperature keeps on increasing as long as dQ/dt > 0. But if you, for example, look at the idealized diurnal evolution of air temperature, it can be seen that the temperature keeps on increasing until its maximum value, despite the fact that there is net heat loss (dQ/dt < 0 for example between noon and 4h where the area between both curves becomes smaller)...
It seems that on the figure here the temperature keeps on rising as long as the value of Q itself > 0 but that doesn't necessarily mean that dQ/dt has to be > 0, right? Is my reasoning wrong or how can this correctly be explained with formulas?
Thanks already!