Tension and ball of mass problem

[Dumbledore211]

Homework Statement

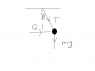
A ball of mass 0.5 kg is attached to one end of a cord of unstretched length 0.6 whose other end is fixed . When a horizontal force of QN is applied to the ball in equilibrium , the cord increases by 10 percent and is inclined at β= arcsin3/5 to the downward vertical. Calculate the value of Q and the modulus of the cord

Homework Equations

T= λx/l where λ= modulus, x=extension and l=natural length

The Attempt at a Solution

I have tried to solve it by using the above eqn and using a right-angled triangle. I think my visualization of the problem is somewhat correct. But I don't think my approach is.

 

[lewando]

Draw the free body (force) diagram. Write down all the equations you can based on all given information and the fact that the ball is not moving. Solve for T before you try to find the modulus.

 

[Dumbledore211]

Do I set up simultaneous equations using T and the modulus as two unknown variables??
we just can't solve for T without using λ as it happens to be the constant proportionality of T.

 

[lewando]

Assume you are using a cord that does not stretch and therefore is unstretched at equilibrium. Solve for T.

If you replace the cord with one that does stretch, does any force component change?

 

[Dumbledore211]

Are you telling me to use a cord that won't have any kind of extension? Could you give me an example as to how I can apply your way in solving this problem..

 

[lewando]

Solved examples for this problem (with an inelastic cord) are available on the internet. I am uncomfortable (per rules) with simply directing you there. I am comfortable working through the solution with you. In both cases (elastic or inelastic cord), they begin with a free body diagram. Can you generate one?

 

[Dumbledore211]

I really can't see how I can do this with an inelastic cord. Do you know where I can find similar examples on the internet to this problem. Your help would be really appreciated if I finally somehow manage to reach a reasonable solution.

 

[Dumbledore211]

Okay, I think there are going to be two separate diagrams. One is the diagram of the whole system affected by the horizontal force Q and the other one is the force Q itself breaking into it's components. Am I going in the right direction with this now?

 

[lewando]

Draw as many diagrams that you have time for that you think might be helpful. For now, I would suggest focusing on the free body diagram of the forces acting on the ball. Q, being a horizontal force applied to the ball, will only have a horizontal component. What are the other forces acting on the ball?

 

[Dumbledore211]

Yes, I have drawn my free body diagram. There is only the mg force that attracts the ball downward except Q. Since we have to find Q, I don't think we have to resolve it. There are
mainly two forces on the ball. One is this Q and the other is mg. But what about the angle?
I think the angle is created between the ball's original and current positions.

 

[lewando]

There is a third force, T from the cord. Since the ball is not accelerating, there is no net force on the ball. Force vectors T, Q, and mg add up to zero. If you can, please post your FBD.

 

[lewando]

... what about the angle?
I think the angle is created between the ball's original and current positions.

Not sure I understand your question. If by "original position" you mean hanging straight down, before Q is applied, and by "current position" you mean the equilibrium state with Q applied, then yes, that is the angle.

 

[Dumbledore211]

Okay, since the ball is not accelerating, can I set the eqn, T=mg and using this information can I find out Q using the expression, Q=Ttanβ??

 

[lewando]

T is not equal to mg. Please post any drawing you have. I want to make sure you understand the fundamental configuration of the system.

 

[Dumbledore211]

I am relatively new in this forum.I really have no idea about posting any sort of diagrams in this thread. Could you tell me which software I should use to post the FBD diagram

 

[lewando]

I see-- if your computer does not have a tool like Paint, you could use an on-line tool like http://drawisland.com/

Some people just draw a picture then scan it if they have a scanner.

There are couple ways to get the image onto your post. Upload it to http://beta.photobucket.com/ which results in a link that you can insert into your post using the Go Advanced tools.

Probably the simplest method is to use the attachment tool (paperclip icon under Go Advanced). There are size limits to this method.

This is a good thing for you to figure out--it will greatly enhance your ability to communicate. Go ahead and experiment with this--don't worry about making a mistake. I don't think you can crash PF.

 

[Dumbledore211]

I have sent the FBD diagram in this attachment file. Check out the digram and see if there is any mistake

 

[lewando]

Looks okay except the force T is pulling on the ball, not pushing.

 

[Dumbledore211]

Oops I am sorry that I made a trivial mistake as I was in a bit of hurry to post it. So, now isn't there going to be a resultant force of Q and T like R=Q+T. Then isn't the equation going to look something like R-mg=ma

 

[lewando]

That's the idea. Basically you sum the forces Q, T, and mg to get ma, where ma is zero because the ball is not accelerating. To save some time, your next step is to break these forces into their x- and y-axis components. Once that is done, you can get 2 equations: the sum of the x-axis forces = 0, and the sum of the y-axis components = 0.

 

[Dumbledore211]

Okay, I have got two simulatneous equations like Tcosα + Qcosα=0 and Tsinα + Qsinα=mg
Now Could you help me with the angles?

 

[lendav_rott]

You can use factoring to determine the angles
For example: Tcosa + Qcosa = 0
I have been warned about throwing direct solutions out, so I think I'm not allowed to say how exactly this works. Anywho, once you've done the factoring you get a product of 0. A product is 0 when one of the factors is 0 - which one of the factors you think would be 0.
You have 2 equations and 2 variables - take into account that cosa = sin(90-a)

 

[lewando]

You are given the angle: β=arcsin(3/5). You should be able to evaluate this with a calculator. This is also a geometric way to express an angle based on a right triangle. Take the sin of both sides: sin(β) = 3/5 = opp/hyp. You should be able to figure out what the "adj" side is.

T is the only force that has x AND y components. Q has only an x component, mg only a y component (x-axis is along the horizontal, y-axis, vertical).

@lendav_rott: not sure I follow you. Perhaps show an example of what you mean.

 

[Dumbledore211]

No, you misunderstood my question. Factoring really makes things a lot more difficult. My question really was "Isn't there any other way to use the given info of the question where the only angle β= arcsin3/5.

 

[Dumbledore211]

Thank you lewando so much for your help. I finally understood clearly how I can solve these problems. I really appreciate the time that you have invested in posting these little hints that really clarified my concept of this problem and finally helped me to reach an answer.

 

[Dumbledore211]

My own explanation of the problem in brief. The x-component of T neutralizes the x component of Q. The y-component of T neutralizes the y-component of mg which is why the ball gains an equilibrium state thereby resulting in zero acceleration of the system.

 

[lewando]

I think you have said that well.