Tension in a pulley system pulled at an angle

In summary, the problem at hand is whether the tension in a system with a 90 degree angle is just 2T or not. It is believed that in a "normal" situation, the tension would be less than 2T and symmetric. Another question is whether making the pulley fixed would affect the tension. The concern is that the vertical rope should not be shown as straight vertical and there may be a sideways force from the right rope that could pull the mass to the right. Finally, there is a request for assistance in creating a free body diagram for the loaded pulley.
  • #1
erensatik
9
3
Homework Statement
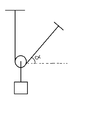
The system is in equilibrium. What is the tension in the bottom rope in the setup below? Neglect the mass of the rope and the pulley.
Relevant Equations
F=ma
This problem just came to my mind when thinking on another problem. Does the tension is just 2T as it is if the angle "a" is 90 degrees? It seems not to me. In a "normal"( I don't really know what is the right word for that) situation, the tension is would be 2T at the line in the middle of two strings and would be symmetric. So it should be less than that I guess. That's all I can think of and I am not sure. Please help me out.
One last thing I need to ask is that does making the pulley fixed makes a difference? I have no idea what would be the difference.
 

Attachments

  • Untitled.png
    Untitled.png
    3.2 KB · Views: 190
Last edited:
Physics news on Phys.org
  • #2
I don't think you should be showing the vertical rope as straight vertical. Do you think that the sideways force from the right rope might pull the mass to the right a bit?
 
  • Like
Likes Lnewqban
  • #3
Do you know how to create a free body diagram of that loaded pulley?
 
  • #4
Lnewqban said:
Do you know how to create a free body diagram of that loaded pulley?
totally got it, saying that is enough. Thanks for the help
 
  • Like
Likes Lnewqban and berkeman

FAQ: Tension in a pulley system pulled at an angle

What is tension in a pulley system pulled at an angle?

Tension in a pulley system pulled at an angle refers to the force exerted on the pulley by the rope or cable that is pulling it at an angle. This force is responsible for keeping the pulley in place and allowing it to rotate smoothly.

How is tension affected by the angle of the pull?

The tension in a pulley system is directly affected by the angle of the pull. As the angle of the pull increases, the tension also increases. This is because the force required to pull the pulley at an angle is greater than the force required to pull it straight up.

What factors can affect the tension in a pulley system pulled at an angle?

Aside from the angle of the pull, the tension in a pulley system can also be affected by the weight of the object being lifted, the friction between the pulley and the rope, and the weight of the pulley itself. These factors can all impact the amount of tension required to keep the pulley in place and lift the object.

How can tension in a pulley system pulled at an angle be calculated?

To calculate the tension in a pulley system pulled at an angle, you will need to know the angle of the pull, the weight of the object being lifted, and the weight of the pulley. You can then use trigonometric functions to determine the amount of tension required to lift the object at the specified angle.

What are some real-world applications of tension in a pulley system pulled at an angle?

Tension in a pulley system pulled at an angle is commonly used in various industries such as construction, engineering, and transportation. It is used in cranes to lift heavy objects, in elevators to move between floors, and in sailboats to adjust the angle of the sails. It is also used in simple machines like a flagpole or a bicycle to help with lifting and moving objects.

Similar threads

Tension in a string which connects 3 pulleys
Replies
12
Views
599
Tension in a complex-pulley-system
Replies
27
Views
2K
2 pullies and 3 masses -Tension
Replies
18
Views
2K
Ideal Vs Real Mass Pulley system
Replies
10
Views
4K
System of two pulleys and three masses
Replies
22
Views
4K
Find the load saved by a pulley system
Replies
15
Views
1K
3 pulley problem with attached masses
Replies
15
Views
4K
Need maximum weight on an extension machine
Replies
2
Views
446
Block and pulley on movable incline
Replies
2
Views
1K
Springs and Pulleys - Force analysis
Replies
18
Views
449

Hot Threads

Recent Insights

Back
Top