foo9008
- 676
- 4
Homework Statement
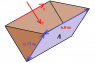
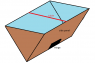
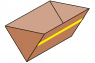
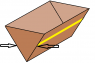
calculate the tension in the cable
Homework Equations
The Attempt at a Solution
the resultant force act on the each metal bar is equal to the tension of each bar . so FR= tension in bar
but , i have problem of finding the the area in FR , i have only (0.75/2) sin45(1000)(9.81) A . For A , i only know the one of the length , how to do this question ?


![DSC_0516[1].JPG](/data/attachments/80/80299-b67cceb34b138377567b54cbff9c6874.jpg?hash=tnzOs0sTg3)