SUMMARY
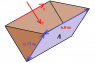
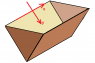
The discussion focuses on calculating the tension in a cable supporting a trough submerged in water, specifically addressing the resultant hydrostatic pressure acting on the trough's sides. Participants clarify that the problem involves rotational equilibrium, where the tension in the cable counteracts the moments created by fluid pressure on the trough's panels. The final calculated tension is determined to be 5518 N, derived from the equilibrium of moments about the hinge point of the trough.
PREREQUISITES
- Understanding of hydrostatic pressure and its calculation.
- Knowledge of rotational equilibrium and torque concepts.
- Familiarity with the geometry of a trough and its dimensions.
- Ability to apply the second moment of inertia in fluid mechanics.
NEXT STEPS
- Study the principles of hydrostatic pressure and its effects on submerged surfaces.
- Learn about rotational equilibrium and how to calculate moments in mechanical systems.
- Explore the application of the second moment of inertia in fluid statics problems.
- Review trigonometric methods for resolving forces in inclined planes.
USEFUL FOR
Students in engineering, particularly those studying fluid mechanics, mechanical engineers, and anyone involved in structural analysis of submerged objects.