Tension in the strings (with diagram)

[AlphaRock]

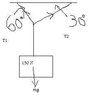
Homework Statement

Find the tension in each string given the diagram.

Homework Equations

Fx = ma.
Fy = ma.

The Attempt at a Solution

Fy = 0. Because it's at equilibrium.
T1(sin30) + T2(sin60) - mg = 0.
T1 = [mg - T2(sin60)]/(sin30)

Fx = 0.
T1(cos30) + T2(cos60) = 0.
T1 = [-T2(cos60)]/(cos30)

T1 = T1
[mg - T2(sin60)]/(sin30) = [-T2(cos60)]/(cos30)
150/(sin30) = -T2[(cos60)/(cos30)] + T2[(sin60)/(sin30)]
150/(sin30) = T2[[(sin60)/(sin30)] - [(cos60)/(cos30)]]
T2 = 259.8 N

Substitute T2 into
T1 = [-T2(cos60)]/(cos30)
T1 = 150 N.

Therefore,
T1 = 150 N.
T2 = 259.8 N
Is this the right answer?

 

[kuruman]

T1(cos30) + T2(cos60) = 0.

You need a minus sign here. One component is positive and the other is negative.