Tension problem with several ropes and a mass

[Andy1234]

I attached an image of the problem but here's an explanation.
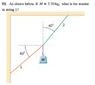
A 5.50kg mass is hanging from a rope that is attached to two other ropes. Rope 1 is 40 degrees below the negative horizontal and Rope 2 is 40 degrees to the right of the positive vertical. Find the tension in rope 1.I understand most tension problems but the one rope in the same direction as the mass is throwing me off. I know that T1 and T2 are equal in the x direction. But that means T1 has a y component that must be canceled out by T2's y compenent. But if T2's y component increases further then doesn't its x also increase? Which will make T1's x and y increase. I don't understand. Please help.

 

[Doc Al]

Don't forget that there are three ropes intersecting at a point.

 

[Andy1234]

Don't forget that there are three ropes intersecting at a point.

But won't that 3rd rope's tension always be mg?

 

[Doc Al]

But won't that 3rd rope's tension always be mg?

Absolutely.

But that means T1 has a y component that must be canceled out by T2's y compenent.

Don't forget that third rope.

 

[Andy1234]

Absolutely.Don't forget that third rope.

But that rope has no x forces so it won't have an effect on the others. I've tried solving this a few different ways. When I get rope 2's tension I get it by setting its y component to mg, find its x component. T1's x component should be the same. But it's not horizontal so it will pull down as well changing rope 2s y component. This is where I run into that issue I explained in the original post.

My other approach was to first get Rope 1's y component by having it equal cos50 * mg. So 2's y component would be mg plus T1's y component. From there solve for the x components. But when I did that I got the wrong answer.

 

[Doc Al]

But that rope has no x forces so it won't have an effect on the others.

But it certainly has a y-component!

My other approach was to first get Rope 1's y component by having it equal cos50 * mg.

No guessing!

Analyze the x and y components acting at the point where they meet. The net force at that point must be what?

 

[SciencyBoi]

I understand most tension problems but the one rope in the same direction as the mass is throwing me off. I know that T1 and T2 are equal in the x direction. But that means T1 has a y component that must be canceled out by T2's y compenent. But if T2's y component increases further then doesn't its x also increase? Which will make T1's x and y increase. I don't understand. Please help.

Your line of thinking is correct, however, there lies exactly a point between the increase of T1 vs T2 such that the balance the whole setup.
(Also, when you increase T1, it's larger component is in the vertical direction, whereas the T2's larger component is in the horizontal direction, which balances things out, because T2 is greater than T1 to begin with, so naturally it had a greater component in the horizontal direction, when you increased T1 to compensate, you basically increased T1 most in the horizontal direction as compared to the vertical direction. (Which again is due to an angle less than 45°))
You can also think of it as two people on a circular track with different speeds. They will eventually meet at the starting point no matter the difference in their speeds.

........ .........
To calculate them, the best method would be to draw a force body diagram. Mark all the forces at the point of the intersection of three ropes and balance then out.

I am not doing the calculation, however, giving a hin(basically the solution)t;
The y direction equation would look like;

Mg + T1 sinθ = T2 cosθ

And x direction equation would look like;
T2sinθ=T1cosθ.

This should help.

 

[Andy1234]

Your line of thinking is correct, however, there lies exactly a point between the increase of T1 vs T2 such that the balance the whole setup.
(Also, when you increase T1, it's larger component is in the vertical direction, whereas the T2's larger component is in the horizontal direction, which balances things out, because T2 is greater than T1 to begin with, so naturally it had a greater component in the horizontal direction, when you increased T1 to compensate, you basically increased T1 most in the horizontal direction as compared to the vertical direction. (Which again is due to an angle less than 45°))
You can also think of it as two people on a circular track with different speeds. They will eventually meet at the starting point no matter the difference in their speeds.

........ .........
To calculate them, the best method would be to draw a force body diagram. Mark all the forces at the point of the intersection of three ropes and balance then out.

I am not doing the calculation, however, giving a hin(basically the solution)t;
The y direction equation would look like;

Mg + T1 sinθ = T2 cosθ

And x direction equation would look like;
T2sinθ=T1cosθ.

This should help.

That makes sense. I tried something similar but got a wrong answer. Probably made a mistake along the way so I I'll try that again.