Tension question (this should be basic)

[pureouchies4717]

tension question on object moving in a circle (this should be basic)

A .6 kg steel block rotates on a steel table while attached to a 1.20 m-long hollow tube. Compressed air fed through the tube and ejected from a nozzle on the back of the block exerts a thrust force of 4.10 N perpendicular to the tube. The maximum tension the tube can withstand without breaking is 50.0 N. (coefficient of kinetic friction:.6) If the block starts from rest, how many revolutions does it make before the tube breaks?

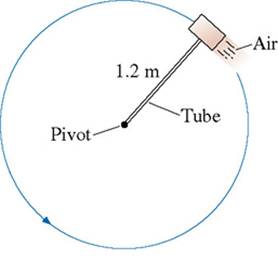
im stumped...

look 1 post down... I am trying

 

[pureouchies4717]

ah i found something:

at= 6.833333 m/s^2

Fr= mat - Ff

Fr= 4.1N- Ff
= 4.1-3.528
=.572N

a(c)= .953333m/s^2

 

[pureouchies4717]

ok here's what i tried:

at 50N, the object is going at:
v= 10m/s

so i plugged this in the T=(mv^2)/r equation and got: T=50s, but this looks wrong, and i don't know how to get revs from this...

 

[pureouchies4717]

hmmm...

angluar velocity= (at/r)t= 284.722rad/s= 2718.89 rpm

2718.89= 45.315 revs/second

45.315 x 50 = 2265.75 revolutions (wrong)

 

[pureouchies4717]

guys please help me, there's only one hour left

 

[Tide]

Here's a start:

The angular acceleration is given by

I \frac {d^2 \theta}{dt^2} = r (F_T - \mu mg)

where I is the moment of inertia (essentially just m R^2). Use the equation solve for the angular velocity and the angular displacement as a function of time then determine the time at which the centripetal force reaches the breaking point.

 

[pureouchies4717]

Here's a start:

The angular acceleration is given by

I \frac {d^2 \theta}{dt} = r (F_T - \mu mg)

where I is the moment of inertia (essentially just m R^2). Use the equation solve for the angular velocity and the angular displacement as a function of time then determine the time at which the centripetal force reaches the breaking point.

thank you , thank you for responding

 

[pureouchies4717]

Here's a start:

The angular acceleration is given by

I \frac {d^2 \theta}{dt^2} = r (F_T - \mu mg)

where I is the moment of inertia (essentially just m R^2). Use the equation solve for the angular velocity and the angular displacement as a function of time then determine the time at which the centripetal force reaches the breaking point.

thanks so much, but i don't really get what youre saying. what does Ft mean? o, i didnt learn about inertia yet

 

[pureouchies4717]

guys, i don't want you to waste your time. if you arent able to help in the next 30 minutes, don't even worry about it