fogvajarash
- 127
- 0
Homework Statement
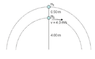
An object of mass m1 of 4.00kg is tied to an object of mass m2 of 3.00kg with a string of length 0.5m. The combination is then swung in a verticular circular path on a second string of length 4.00m. The two strings are always colinear (they are on the same line). At the top of the motion, m2 has a speed of 4.00 m/s. Now, answer the following:
a. What is the tension in the short string (the 0.5m string) at this moment?
b. What is the tension in the long string (the 4.00m string) at this moment?
c. If you rotate the system faster and faster, which string (assuming they have identical strengths) breaks first?
Homework Equations
-
The Attempt at a Solution
I have no idea how to approach this problem. I keep getting a negative tension while doing this exercise: I've talked to a friend and we keep getting the same result. Our FBD for the first mass (the farthest one) is just one tension and its weight. On the other hand, for the second mass (the closest one) is the tension upwards, the other downwards and the weight. These two forces provide the centripetal force which makes them go in a circle.