- #1
vanitymdl
- 64
- 0
Y: 51 32 30 74 42 35 39 33 55 61
Y-hat: 49 35 29 72 44 32 38 36 57 60
Null hypothesis: mean y-hat = mean y
Alternative hypothesis: not null hypothesis
So I got as a t test 0 and I was wondering if I did something wrong because I never has this case happened to me.
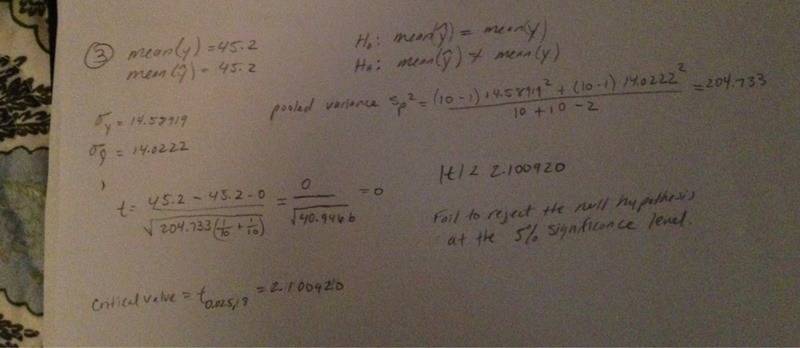
Y-hat: 49 35 29 72 44 32 38 36 57 60
Null hypothesis: mean y-hat = mean y
Alternative hypothesis: not null hypothesis
So I got as a t test 0 and I was wondering if I did something wrong because I never has this case happened to me.