Luis2101
- 13
- 0
Two loudspeakers, A and B, are driven by the same amplifier and emit sinusoidal waves in phase. Speaker B is 2.00 m to the right of speaker A. Consider point Q along the extension of the line connecting the speakers, 1.00 m to the right of speaker B. Both speakers emit sound waves that travel directly from the speaker to point Q.
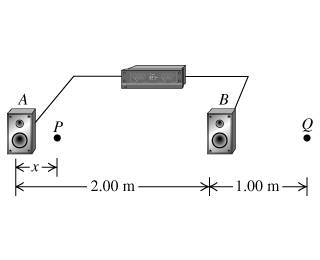
A)What is the lowest frequency for which constructive interference occurs at point Q?
B)What is the lowest frequency for which destructive interference occurs at point Q?
------
Grr... my professor flew through this section in our lecture so I'm pretty lost and have this problem due. Basically all I know so far is that if the amplitude is 2yo or phi is n(2pi) the wave is constructive... But I've no idea where to go from there.
Really, any help would be greatly appreciated.
-Luis
A)What is the lowest frequency for which constructive interference occurs at point Q?
B)What is the lowest frequency for which destructive interference occurs at point Q?
------
Grr... my professor flew through this section in our lecture so I'm pretty lost and have this problem due. Basically all I know so far is that if the amplitude is 2yo or phi is n(2pi) the wave is constructive... But I've no idea where to go from there.
Really, any help would be greatly appreciated.
-Luis