madinsane
- 31
- 0
Homework Statement
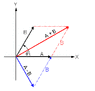
Two vectors A and B have precisely equal magnitudes. In order for the magnitude of A+B to be 120 times larger than the magnitude of A-B , what must be the angle between them?
Homework Equations
None (i think)
The Attempt at a Solution
A+B=120(A-B)
(xi+yi)+(xi+yi)
2x+2y=120(2x+2y)
2x+2y+240x-240y
Then I don't know where to go from here
Is what I am doing even correct?
Point me in the right direction