The formula for a tangent plane to a surface

[Mazzur]

Hey I'm trying to understand how we arrive at the formula for the tangent plane to a surface. An image of what I'm talking about it shown below.

I think understand all the parts up to part c, but i don't see how we arrive at that final formula. The image of first part of the solution is shown just to provide context.

 

[tiny-tim]

Welcome to PF!

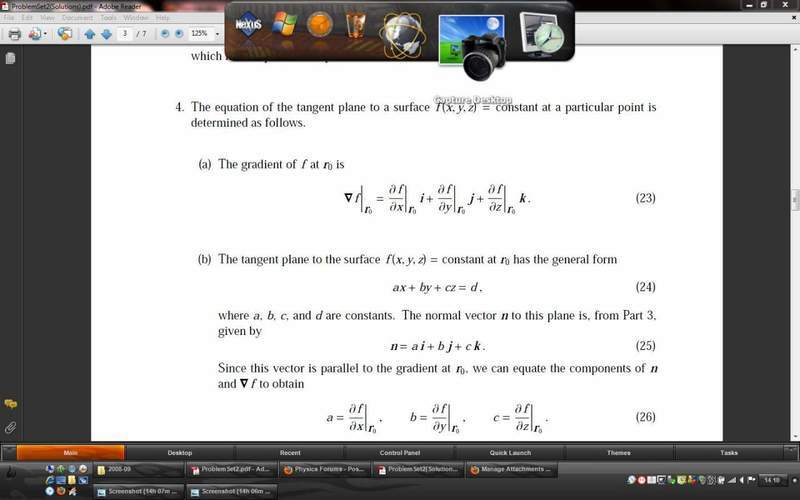
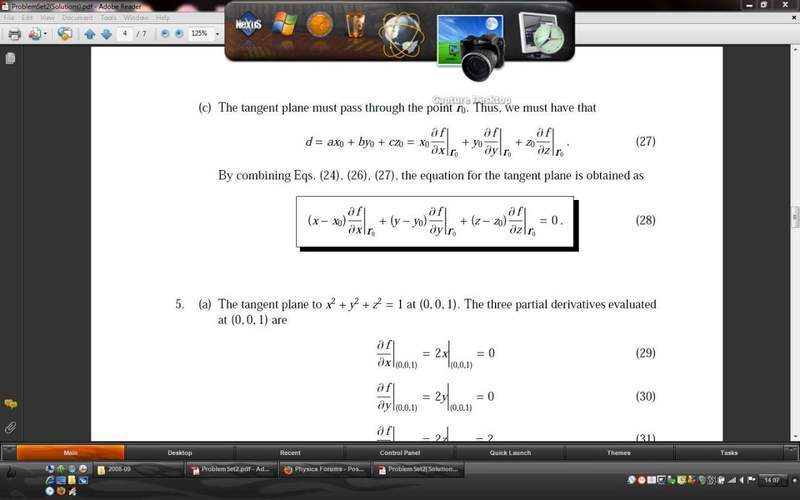
I think understand all the parts up to part c, but i don't see how we arrive at that final formula.

Hey Mazzur! Welcome to PF!

∂f/dx|_ro ∂f/dy|_ro and ∂f/dz|_ro are all constants, and they are the constants that have to be the coefficients of x y and z …

that's the bit you understand, isn't it?

So the equation has to be
∂f/dx|_rox + ∂f/dy|_ro y + ∂f/dz|_roz = constant,

and all they've done is to put that constant on the left of the = sign, and split it up between the three coordinates.

If you prefer, you can put it back on the right, like this …

∂f/dx|_rox + ∂f/dy|_ro y + ∂f/dz|_roz = ∂f/dx|_rox_o + ∂f/dy|_ro y_o + ∂f/dz|_roz_o …

either way, you can see that putting x = x_o, y = y_o, z = z_o, makes the equation true.