A The hermicity of a k.p matrix?

[lichen1983312]

I am trying to use the k.p method to study quantum well band structure. One example Hamiltonian look like this [J. Appl. Phys., 116, 033709(2014)]

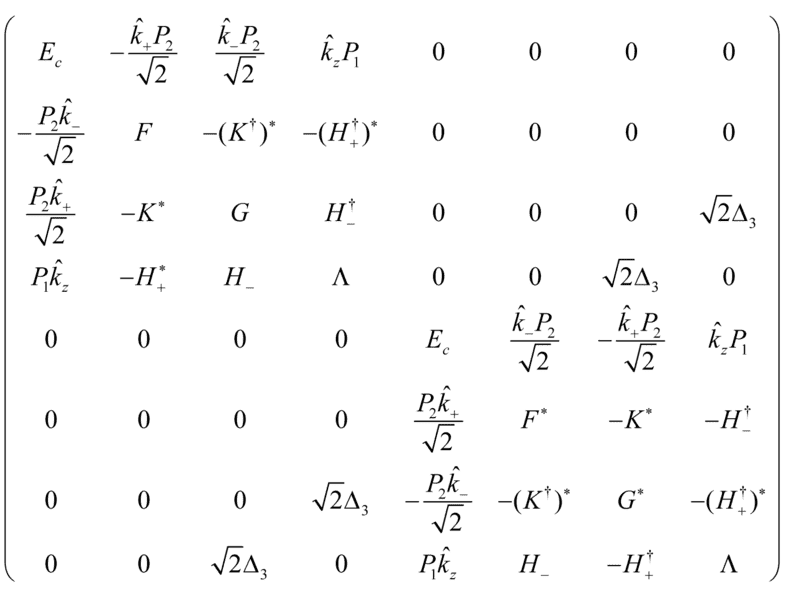where
${{\hat k}_ \pm } = {{\hat k}_x} \pm i{{\hat k}_y}$
and the matrix elements are function of ${{\hat k}_i}$
and if quantum well is grown along z direction
the envelop functions have the form
\[F(x,y,z) = {e^{i{{\bf{k}}_\parallel } \cdot {\bf{r}}}}f(z)\]

and therefore

$\left\{ \begin{array}{l} {{\hat k}_x} = - i\frac{\partial }{{\partial x}} \to {k_x}\\ {{\hat k}_y} = - i\frac{\partial }{{\partial y}} \to {k_y}\\ {{\hat k}_z} = - i\frac{\partial }{{\partial z}} \end{array} \right.$

this Hamiltonian is an hermitian operator, but I am confused about this. For example, if I look at the (1,4) and (4,1) terms and use ${{\hat k}_z}=-i{\partial _z}$, the (1,4) term becomes
$-i{\partial _z}{P_1}$
and the (4,1) term becomes
$- i{P_1}{\partial _z}$

If I use finite difference method to turn these two terms into a matrix block, the factor -i is not going to flip sign and the matrix cannot he a hermitian matrix?

there must be something wrong with my understanding, please help.

 

[Dr Transport]

I have to look at the paper first, the matrix is hermitian, but I will say that P_1 and P_2 are constants, not operators if I remember my \vec{k} \cdot \vec{p} theory correctly.

 

[lichen1983312]

I have to look at the paper first, the matrix is hermitian, but I will say that P_1 and P_2 are constants, not operators if I remember my \vec{k} \cdot \vec{p} theory correctly.

Thanks very much, the reference is this one :
https://aip.scitation.org/doi/10.1063/1.4890585