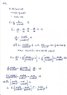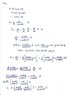The path of the 3.6-kg particle P is an ellipse

AI Thread Summary
The discussion revolves around calculating the polar components of the force acting on a 3.6-kg particle moving in an elliptical path defined by the equation R = R_0 / (1 + e cos θ), with R_0 set at 0.5m and eccentricity e at 2/3. The angular speed of the line OP is constant at 20 rad/s. Participants review the calculations, noting an error in equation (6) that needs correction. Overall, the conversation focuses on verifying the accuracy of the equations used in the problem-solving process. Accurate calculations are essential for determining the forces acting on the particle at point A.
Alexanddros81
Messages
177
Reaction score
4

Homework Statement


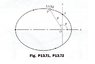
13.71 The path of the 3.6-kg particle P is an ellipse given by ##R = \frac {R_0} {(1+ecosθ)}##.
where R_0 = 0.5m and e=2/3. Assuming that the angular speed of line OP is constant
at 20 rad/s, calculate the polar components of the force that acts on the particle when it is at A.

Fig P13_71.jpg


Homework Equations

The Attempt at a Solution



Pytels_Dynamics085.jpg


Pytels_Dynamics086.jpg


Can you check this?
 

Attachments

  • Fig P13_71.jpg
    Fig P13_71.jpg
    6.3 KB · Views: 517
  • Pytels_Dynamics085.jpg
    Pytels_Dynamics085.jpg
    26.7 KB · Views: 508
  • Pytels_Dynamics086.jpg
    Pytels_Dynamics086.jpg
    9 KB · Views: 400
Physics news on Phys.org
Everything looks good except equation (6), which has an error.
 
Pytels_Dynamics090.jpg

Pytels_Dynamics091.jpg


Can you check this?
 

Attachments

  • Pytels_Dynamics090.jpg
    Pytels_Dynamics090.jpg
    26.6 KB · Views: 349
  • Pytels_Dynamics091.jpg
    Pytels_Dynamics091.jpg
    10 KB · Views: 338
Looks good.
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Use angular momentum to find the velocity (comet orbit)
Replies
14
Views
2K
Energy analysis of a particle moving in a shrinking circle
Replies
17
Views
4K
How Does Particle P Chase Particle Q on a Circular Path?
Replies
35
Views
5K
Angular Momentum of a Moving Particle
Replies
2
Views
1K
Angular momentum of particle about the origin
Replies
7
Views
2K
Kinetic Energy for particles (alpha decay)
Replies
2
Views
3K
Conservation of Angular Momentum of Train on Disk
Replies
6
Views
3K
Calculating Kinetic Energy with Rotational Motion
Replies
3
Views
6K
Kinetic energy of rotation and parallel axis theorem problem
Replies
11
Views
3K
A Particle moving on a constrained path
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top