B Why Does the Effective Period of a Composite Wave Remain Constant?

[roam]

TL;DR Summary

I am trying to understand whether the period of a composite wave relates to the relative phases or the number of the constituent waves.

I am working with a simulation which generates multiple identical functions that overlap differently (i.e., they are generated with randomly different phases from each other).

When I calculate the composite wave, the shape of the combined wave will differ depending on the relative phases of the input waves. But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that? What would be an analytic expression that explains this phenomenon?

For instance, this is the simulation using three waves (the thicker line is their sum):

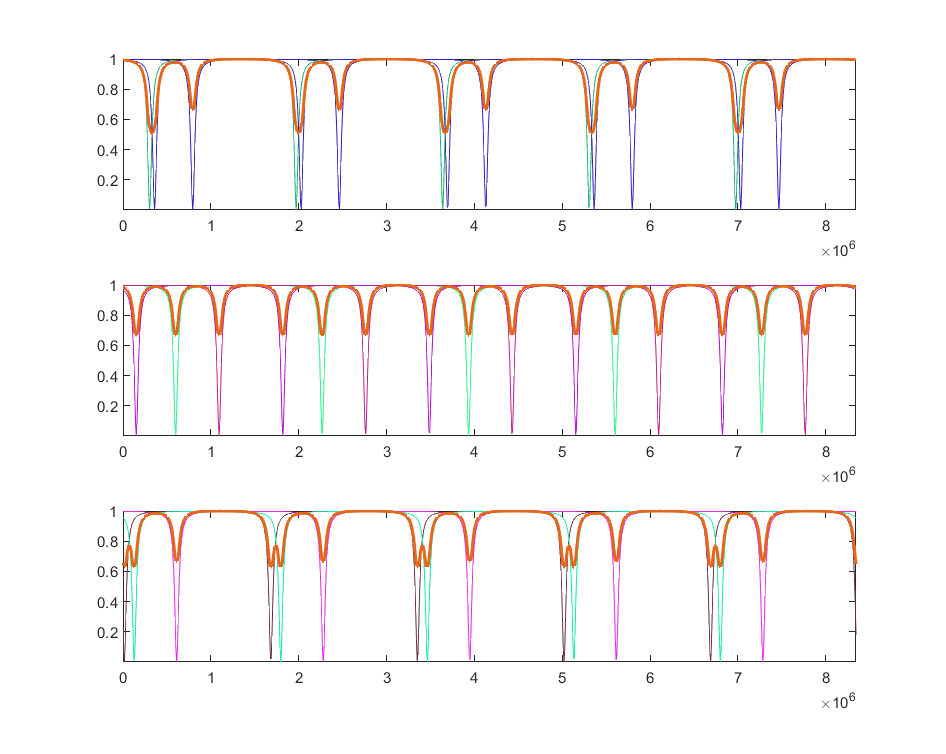
In addition, if we increase the number of waves, the temporal period of the combined wave will still remain constant. Why?

Here is an example:

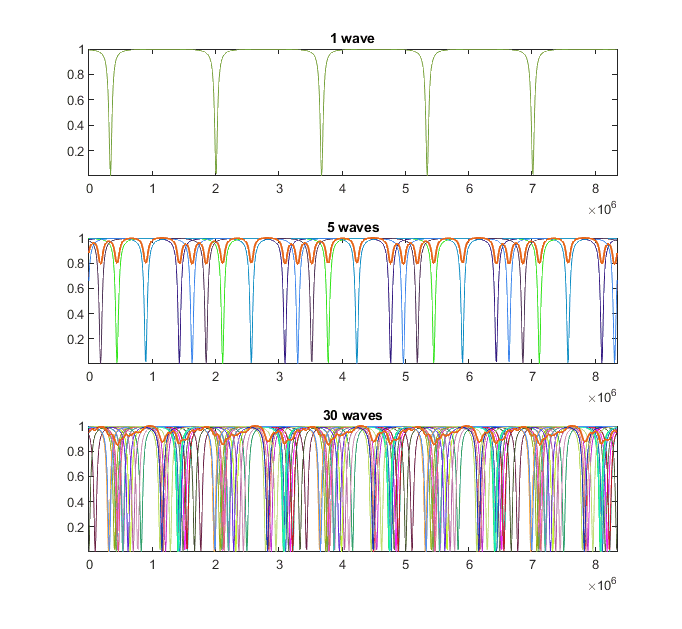
Any explanations would be appreciated.

 

[DrClaude]

I don't understand what these "waves" are. It seems to be simply a peaked function that is repeated periodically.

Also, the thicker line doesn't appear to be the sum of the other curves, but rather the average value of the sum.

When I calculate the composite wave, the shape of the combined wave will differ depending on the relative phases of the input waves. But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that? What would be an analytic expression that explains this phenomenon?

If the underlying phenomena have the same period, then any linear combination of them will have the same period.

 

[roam]

Hi DrClaude,

I don't understand what these "waves" are. It seems to be simply a peaked function that is repeated periodically.

Also, the thicker line doesn't appear to be the sum of the other curves, but rather the average value of the sum.

The function I am using is the complementary Airy function that gives the ratio of light reflected from an interferometer.

The thick line is the normalized sum of the individual curves.

If the underlying phenomena have the same period, then any linear combination of them will have the same period.

Do you know of an analytic expressions that shows that the combination will always have the same period (regardless of the phases or the number of the individual constituents)?

 

[DrClaude]

Consider a set of functions $\{ f_i(x) \}$ of period $a$, i.e., $f_i(x+a) = f_i(x)$. Taking $F(x)$ as a linear combination of such functions,
$$
F(x) = \sum_{i=1}^{n} c_i f_i(x)
$$
then
$$
F(x+a) = \sum_{i=1}^{n} c_i f_i(x+a) = \sum_{i=1}^{n} c_i f_i(x) = F(x)
$$
therefore $F(x)$ is periodic with period $a$.

 

[sophiecentaur]

I would say that the 'period' of a periodic function is (strictly) the interval between points when the waveform repeats. If the waveform consists of a number of functions, each of which has its own identifiable period (sine waves or strings of pulses, for instance), then the period of the composite function would be the lowest common multiple of the individual functions. This could be a very long period if the periods have, say periods of large prime numbers of seconds. This would, for instance, correspond to the 'beat' between two sine waves.

 

[jbriggs444]

This could be a very long period if the periods have, say periods of large prime numbers of seconds.

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

 

[roam]

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

This is an interesting point. So, if there are more than two individual signals present, then the ratio of the periods of each pair of signals must be rational. Otherwise, the signal will not be periodic. Is that correct?

Also, do you think this happens often in real life where the two signals have incommensurable periods?

 

[sophiecentaur]

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

I don’t think the term “irrational” is applicable here.
“Irrational” measurements don’t occur. All you can expect is a long recurrence in the ratio of the periods. (Longer than any possible experiment could last.)

 

[DrClaude]

I don’t think the term “irrational” is applicable here.
“Irrational” measurements don’t occur. All you can expect is a long recurrence in the ratio of the periods. (Longer than any possible experiment could last.)

Oh, come on! Who said anything about measurements? This is about the sum of mathematical functions.

 

[sophiecentaur]

Oh, come on! Who said anything about measurements? This is about the sum of mathematical functions.

I have to agree. But the OP is discussing numerical simulation, which is where I got the idea of practicality.

 

[roam]

I am simulating a physical situation where optical fibers can host more than one spatial modes. From what I understood, if you don't experimentally see a period to such a signal on an oscilloscope, it could be the case that the ratio of the period of the constituent modes is not rational (or rather it has a longer recurrence than the length of the experiment).

 

[sophiecentaur]

not rational (or rather it has a longer recurrence than the length of the experiment)

Bearing in mind that you can't produce irrational numbers in a numerical simulation, we should settle for 'a very long repeat time', I think.

 

[jbriggs444]

the ratio of the periods of each pair of signals must be rational. Otherwise, the signal will not be periodic. Is that correct?

For all practical purposes, yes, that would be correct.

Mathematically, there is a loophole. Suppose that you have two signals with period x that sum to zero and a third signal with period kx for some irrational number k. Then the sum of all three signals will be periodic despite two component signals having periods with an irrational ratio.

 

[sophiecentaur]

I think we’re in the fuzzy, oxymoron region here - between axiomatic arguments and practical experience. I don’t Think the thread can reveal much more.

 

[Dullard]

I'm still trying yo figure out how a ratio could ever be 'irrational.'

 

[DrClaude]

I'm still trying yo figure out how a ratio could ever be 'irrational.'

What about $\sqrt{2}/2$?

 

[Dullard]

OK. I should have said: A ratio of periods. Can the period of a waveform be irrational?

 

[DrClaude]

OK. I should have said: A ratio of periods. Can the period of a waveform be irrational?

See for instance
https://www.physicsforums.com/threa...give-incommensurate-potential-periods.968851/

 

[sophiecentaur]

What about $\sqrt{2}/2$?

Point!

 

[sophiecentaur]

What about $\sqrt{2}/2$?

In the case of a one dimensional quantity like frequency, is there a way that an irrational frequency can occur? You can get a line that is 'exactly' √2 inches long but only in a two dimensional figure.
Also, I was thinking about transcendental numbers like e and π. Apart from passing through values involving, say e, can you get a steady frequency of e X 10⁶ Hz? This is a question for someone well versed in Analysis, I think.

 

[jbriggs444]

In the case of a one dimensional quantity like frequency, is there a way that an irrational frequency can occur?

If we grant the assumption that frequencies are precisely knowable then the natural assumption would be that irrational frequencies are the norm and that rational frequencies are the exception. Viewed on a one-dimensional dartboard of real numbers, the rational numbers are a target set of measure zero.

But let us make it practical. If I have a piano string with a density of 2 grams per centimeter and a second piano string with a density of 1 gram per centimeter with both strings the same length and tension then the ratio of the frequencies should be $\frac{\sqrt{2}}2$

Assuming I am not being a bonehead interpreting the string frequency formula.

 

[Paul Colby]

I am simulating a physical situation where optical fibers can host more than one spatial modes. From what I understood, if you don't experimentally see a period to such a signal on an oscilloscope, it could be the case that the ratio of the period of the constituent modes is not rational (or rather it has a longer recurrence than the length of the experiment).

Okay, so optical frequencies are like $10^{14}$ hertz or more. My scope cuts out around $10^8$ Hertz. Can I ask where you purchased yours?

 

[sophiecentaur]

If we grant the assumption that frequencies are precisely knowable then the natural assumption would be that irrational frequencies are the norm and that rational frequencies are the exception.

But let us make it practical. If I have a piano string with a density of 2 grams per centimeter and a second piano string with a density of 1 gram per centimeter with both strings the same length and tension then the ratio of the frequencies should be $\frac{\sqrt{2}}2$

Assuming I am not being a bonehead interpreting the string frequency formula.

I can see where you're coming from and the Maths makes you right but you are talking in purely theoretical terms.
I seem to remember that , from Archimedes, it can be shown that between any two rational numbers there will always be an irrational number which lies in between them. So with your Maths hat on, you have to be right. This implies that signals of any two frequencies, generated totally independently, would have an indeterminately long repeat period.
Frequencies, generated from the same frequency reference, will have rational values (on that reference scale), though.

 

[jbriggs444]

it can be shown that between any two rational numbers there will always be an irrational number which lies in between them

Yes. And vice versa. Both the rationals and the irrationals are dense in the reals. No matter where you land a dart, there will be both irrational and rational numbers arbitrarily close.

From a practical point of view, this means that in any experiment with any margin of error, no matter how small, the measured result will be consistent with infinitely many true values that are rational and infinitely many true values that are irrational. [Making the notion of a "true value" rather questionable].

But that takes all the fun out of the game. So I'm putting my funny looking math hat back on.

 

[sophiecentaur]

So I'm putting my funny looking math hat back on.

I know a number of Maths teachers and worked with a number of Mathematicians. They were nice people but slightly (in some cases, even more than slightly) nutty. I think the subject has a way of getting its own back on Mathematicians. How can you be rational when at least half of the stuff you are dealing with is irrational?

 

[Paul Colby]

In many ways, periodic functions are a fiction, a useful mathematical abstraction used to describe nature under limited circumstance. Since the universe is finite in time, there are no truly periodic functions.

 

[tade]

But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that?

The good doctor has already explained it, but anyway, to the contrary, you should expect the effective period to remain the same, and in fact, it would be very surprising if it didn't.

 

[Paul Colby]

I don't know about anyone else, but the question raised in #2 wasn't addressed AFAIK. A reflection coefficient is not a wave. What's plotted in #1 appears to be the magnitude of the reflection (transmission?) coefficient for X where X is what exactly?

 

[sophiecentaur]

I don't know about anyone else, but the question raised in #2 wasn't addressed AFAIK. A reflection coefficient is not a wave. What's plotted in #1 appears to be the magnitude of the reflection (transmission?) coefficient for X where X is what exactly?

You're right. If there's reflection then the time and spatial variations come into it. Or is it just the repeating interference pattern due to two signal paths that's being discussed? I don't see how any such diffraction patterns will ever repeat over a wide angle.

 

[Paul Colby]

Yeah, I agree. The reason to ask is this impacts what operations are done on said "signal". Looks like maybe a scanning fiber interferometer of some sort where (I'm guessing) the "waves" are fiber modes. A great deal more need be supplied IMO.

 

[roam]

Okay, so optical frequencies are like $10^{14}$ hertz or more. My scope cuts out around $10^8$ Hertz. Can I ask where you purchased yours?

I am simulating fiber ring resonators which basically behave as Fabry-Perot interferometers. What I am plotting is the output of the ring given by the Airy function. The frequency spacing between the adjacent resonance dips (i.e. the period, also known as the free spectral range) is typically ~1-2 MHz for a 100 m loop. When you have multiple modes, they will each have a slightly different period.

 

[sophiecentaur]

When you have multiple modes, they will each have a slightly different period.

This seems to be a general principle in Physics; it corresponds with the fact that the Overtones in many resonant systems are not, in fact, harmonics due to 'end effects' (whatever that means in some cases)

 

[sysprog]

I'm still trying yo figure out how a ratio could ever be 'irrational.'

A ratio being an irrational number may look contradictory at first pass, but rational numbers are those which can be expressed as ratios of integers, and not all ratios can be so expressed; real numbers which can't be so expressed are called irrational, even if they are real ratios, e.g., the ratio of the circumference of a circle to its diameter is an irrational number: $\frac c d =\pi$.

 

[sophiecentaur]

A ratio being an irrational number may look contradictory at first pass, but rational numbers are those which can be expressed as ratios of integers, and not all ratios can be so expressed; real numbers which can't be so expressed are called irrational, even if they are real ratios, e.g., the ratio of the circumference of a circle to its diameter is an irrational number: $\frac c d =\pi$.

I think the problem we are having here is that we are told by Mathematicians about the set of real numbers but we do not actually 'see' quantities that are not rational. Yes, the diagonal of a 1cm square is irrational but we could never cut a piece of wood that's √2 cm long. Our minds work in a quantised world (except when we step into the Maths Jungle) and, of course, any quantised value is, in the end, rational.
This sort of problem goes way back and 'squaring the circle' has bothered people for hundreds of years.

 

[Paul Colby]

I am simulating fiber ring resonators which basically behave as Fabry-Perot interferometers.

Thanks, this should have been the sentence to start the thread. The degree to which one may abstract your question depends on what you actually mean by "signal" "wave form" even function is too vague in this case IMO.

So, at the heart of your simulation is a truly linear system, time harmonic or band limited EM waves in a fiber. Your signal is a time averaged normalized intensity (absolute square) of the interferometer output as a function of interferometer length. The scan frequency is not relevant, it's just a means of reading out the data.

We (well, I actually) can only guess as to what this simulation contains in the way of assumptions or details. Just in general terms the guide or fiber wavenumber will depend on the mode in a complex way depending on nearly everything. There is no reason to expect the ratio of these mode wave numbers to be integer or rational values.

 

[roam]

I seem to remember that , from Archimedes, it can be shown that between any two rational numbers there will always be an irrational number which lies in between them. So with your Maths hat on, you have to be right. This implies that signals of any two frequencies, generated totally independently, would have an indeterminately long repeat period.
Frequencies, generated from the same frequency reference, will have rational values (on that reference scale), though.

Hi @sophiecentaur

So, for my situation would you say that the individual signals whose sum makes up the final signal are generated independently? They have randomly different phases and frequencies, but they are generated by the same underlying function which means that the individual points of the final sum are not independent.

From the measurements that I made, I was never able to detect a period from large core fibers (hosting a few hundred modes). So I think that either means the ratio is "irrational", or the least common multiple is too large. For example, here is an experimental measurement (a single mode on the left, and many modes on the right):

Thanks, this should have been the sentence to start the thread. The degree to which one may abstract your question depends on what you actually mean by "signal" "wave form" even function is too vague in this case IMO.

So, at the heart of your simulation is a truly linear system, time harmonic or band limited EM waves in a fiber. Your signal is a time averaged normalized intensity (absolute square) of the interferometer output as a function of interferometer length. The scan frequency is not relevant, it's just a means of reading out the data.

We (well, I actually) can only guess as to what this simulation contains in the way of assumptions or details. Just in general terms the guide or fiber wavenumber will depend on the mode in a complex way depending on nearly everything. There is no reason to expect the ratio of these mode wave numbers to be integer or rational values.

Hi @Paul Colby

Thanks a lot for the explanation. I have another question. If one of the underlying curves is given by $T(\omega)$, would it be mathematically correct to express the final (superposition/average) signal by the integral $TOT=\int_{\omega_{a}}^{\omega_{b}}T\left(\omega\right)d\omega$? This is for some frequency band $\omega_{a}-\omega_{b}$.

 

[Paul Colby]

I have another question.

I would say no because $T(\omega)$ is the ratio of field amplitudes. The output field of the device at $\omega$ is $E_{\text{out}}(\omega)=T(\omega)E_{\text{in}}(\omega)$. The output intensity is the absolute square of $E_{\text{out}}$. Only the fields are linear. Try writing out the full expression for just two $\omega$. Justify to yourself that all cross terms your proposed integral just drops. Hint, they won't.

 

[roam]

I would say no because $T(\omega)$ is the ratio of field amplitudes. The output field of the device at $\omega$ is $E_{\text{out}}(\omega)=T(\omega)E_{\text{in}}(\omega)$. The output intensity is the absolute square of $E_{\text{out}}$. Only the fields are linear. Try writing out the full expression for just two $\omega$. Justify to yourself that all cross terms your proposed integral just drops. Hint, they won't.

But $T$ is the squared modulus of the ratio of output to input, i.e.,

$$T=\left|\frac{E_{out}}{E_{in}}\right|^{2}.$$

When the final signal is the combination of several different $T$ curves, can't you express it using the integral notation? (I think I've seen that in some other areas)

 

[Paul Colby]

But $T$ is the squared modulus of the ratio of output to input

Not where I come from. I can see why you're having issues. Defining $T$ as the absolute square is like using $R^2$ for resistance in circuit analysis, it would make no sense.

 

[roam]

Not where I come from. I can see why you're having issues. Defining $T$ as the absolute square is like using $R^2$ for resistance in circuit analysis, it would make no sense.

But that's a very common definition of $T$ used in optics textbooks (e.g. §9 of "Optics" by Hecht) or many journal articles such as this one.

 

[sophiecentaur]

But that's a very common definition of $T$ used in optics textbooks (e.g. §9 of "Optics" by Hecht) or many journal articles such as this one.

It's a consequence of the 'confusion' between Power and Field strength. R(esistance) is not a ratio of squares but T (in that paper) is defined as a ratio of squares. Even in PF contributions, it is often necessary to define out terms, to avoid needless arguments.
I must say, using a squared ratio (positive sign) makes it hard to produce a meaningful SUM in calculations when phasors are involved. There must be a good reason why they get away with T always being positive.

 

[Paul Colby]

There is nothing magic in choosing symbols. The paper chooses them poorly IMO but carefully defines their meaning. Equation six refers to T as the "intensity transmission factor". If you treat it like an amplitude transmission factor, you will often get wrong or misleading answers. If the light you are dealing with is monochromatic or incoherent this might be fine. Does your simulation assume various modes are mutually coherent? If a phase relation is assumed between two modes, then the output of the ring is not the sum of intensities. Using T will yield a meaningless number. It all depends on the physics being simulated which remains a mystery to me even now.

[added] If the problem you are working is generalizing the paper to more than a single fiber mode then each fiber mode would (could) be driven by a single common coherent laser mode. In this case I would not expect the output intensity to be the sum of the mode intensities.

 

[roam]

There is nothing magic in choosing symbols. The paper chooses them poorly IMO but carefully defines their meaning. Equation six refers to T as the "intensity transmission factor". If you treat it like an amplitude transmission factor, you will often get wrong or misleading answers. If the light you are dealing with is monochromatic or incoherent this might be fine. Does your simulation assume various modes are mutually coherent? If a phase relation is assumed between two modes, then the output of the ring is not the sum of intensities. Using T will yield a meaningless number. It all depends on the physics being simulated which remains a mystery to me even now.

[added] If the problem you are working is generalizing the paper to more than a single fiber mode then each fiber mode would (could) be driven by a single common coherent laser mode. In this case I would not expect the output intensity to be the sum of the mode intensities.

Hi @Paul Colby

Yes, that is precisely what I am trying to do. In that paper they are only considering rings made of standard telecommunications SMF. I am simulating a situation where there is more than one mode present. The output intensity that you receive with a photodiode on an oscilloscope is the combined effect due to the intensity of individual modes.

The modes are driven by the same laser source, but they each travel at a different speed depending on their group refractive index.

What I had done in my simulation was to add the individual $T$ values (i.e., for $M$ modes I had $T_{\text{Total}}=\left|\frac{E_{2}}{E_{1}}\right|_1^{2}+...+\left|\frac{E_{2}}{E_{1}}\right|_{M}^{2}$).

If I understood correctly, the right approach would be to compute all the individual $\frac{E_{2}}{E_{1}}$ curves, add them all together, and then take the absolute square of the sum to find intensity?

So we could write:

$$T=\left|\left(\frac{E_{2}}{E_{1}}\right)_{1}+...+\left(\frac{E_{2}}{E_{1}}\right)_{M}\right|^{2}$$

Is that correct?

 

[Paul Colby]

Is that correct?

No. Amplitude ratios are no more linear than intensity ratios. If I understand the very brief glimpse of the paper the ring is coupled to a fiber line via a coupler. With multimode fiber, one will get varying phase and amplitudes in each mode. Each complex fiber mode (amplitude with phase) will get multiplied by its own coefficient and the result summed. Your expression assumes all these amplitudes are equal in magnitude and phase. This assumption isn't even close to true for a real coupler IMO.

 

[Paul Colby]

I might just comment on common practice in optics. For telescopes imaging incoherent light the intensity transfer function or MTF is indeed a sum of intensities. this happens because a telescope is linear in intensity. Basically

$\langle E(\omega_1)E(\omega_2)\rangle = I(\omega)\delta(\omega_1-\omega_2)$

In this case the $\langle\rangle$ are time averaging of the fields. Adding two fields at different frequencies the cross terms vanish in very short order making the resulting intensity the sum.

As with everything it's vital to understand the underlying principles and not just apply the "usual tricks". Optics is rife with these IMO.

 

[roam]

Hi @Paul Colby

I am slightly confused. I want to make sure I understood you correctly. Could you please write the expression for the sum that you think is valid?

My simulation already accounts for the modes acquiring different phases. I could also assign each mode with a different amplitude.

The plot in my post #36 is an actual measurement, which is what I am trying to simulate with the sum. I'm only trying to get a basic first-order picture. A more rigorous approach would have to account for phenomena such as modal coupling, etc.

 

[Paul Colby]

There is no plot in #36? Only #1 shows any plots. None appear to be a measurements?

The problem I have with writing out an expression even in principle is it's too complex a linear system to do off the cuff. From what you've asked so far I have little confidence you understand basic network theory. Explaining this here is much to ask but I would suggest introductory books on RF and microwave design. Sections on S and T matrix treatments of waveguides would be applicable.

The coupler in the paper is a 4-port device for single mode fiber becomes a 4N-port device where for common multimode fiber N is greater than 100. Of the $10^4$ S-matrix parameters only a handful are likely known even partially. I would also expect these to not be well controlled for a multimode coupler.

Good luck.

 

[roam]

Here is the picture of sample measurements from my post #36.

Okay. But I think you may be assuming that the spatial modes are coherent. They oscillate at different frequencies since they each experience a different group index. That means the cross term averages to zero, and you can add individual intensities.

 

[sophiecentaur]

So, for my situation would you say that the individual signals whose sum makes up the final signal are generated independently? They have randomly different phases and frequencies, but they are generated by the same underlying function which means that the individual points of the final sum are not independent.

Can I get this straight? It seems to me that the device you are talking about is not a source but a complicated filter with roughly but not perfectly harmonically related nulls / modes. I don't understand where the concept of coherent modes comes in.

 

[Paul Colby]

Here is the picture of sample measurements from my post #36.

Okay. But I think you may be assuming that the spatial modes are coherent. They oscillate at different frequencies since they each experience a different group index. That means the cross term averages to zero, and you can add individual intensities.

Sorry, I thought you wanted to generalize the formalism in the paper you linked to on ring resonators for multiple transmission line modes. Ring resonators are passive linear devices which don’t alter the input frequency in any way whatsoever.

A simpler example is single versus multi mode fiber. If fed with a monochromatic source neither modifies the frequency of the light, ever.