The time for 2 light pulses in a moving vehicle

[powermind]

Hi,
Car is moving at speed v. The pulse is sent inside from the back to the front. It takes time t. Another pulse is sent from the front to the back and takes same t. How should outside observer expect? Does he find that the two pulse hit sides at the same time? It sounds no. How can you apply time dilation equation for this example?

 

[PeterDonis]

Hi powermind, and welcome to PF!

Car is moving at speed v. The pulse is sent inside from the back to the front. It takes time t. Another pulse is sent from the front to the back and takes same t.

Assuming that these times are in the car's rest frame, yes, this is correct. But in a frame in which the car is moving, the times taken are different. See below.

How should outside observer expect? Does he find that the two pulse hit sides at the same time?

No. Actually, "at the same time" here is ambiguous, because you didn't specify when, in the car's rest frame, each pulse is sent. If we assume that the pulses are sent from each end of the car at the same time $t_0$ in the car's rest frame, then as above, they both are received at the opposite ends of the car at the same time, $t_0 + t$, in the car's rest frame. However, in a frame in which the car is moving at speed $v$, the pulse from the car's back end will be sent first, before the pulse from the car's front end; but the pulse from the car's front end will be *received* first (at the car's back end), *before* the pulse from the car's back end is received at the car's front end.

How can you apply time dilation equation for this example?

You don't need to to figure out the things I stated above: all you need to know is that both light pulses travel at the same speed in both frames, and that the Einstein definition of simultaneity applies. The latter is needed to obtain the fact that an observer at the center of the car, and riding along in it (i.e., at rest relative to the car), will see both light pulses pass him at the same instant. Once you have those facts, everything else follows.

The only role time dilation might play is to explain how it can be that the light pulses travel at the same speed with respect to both frames (the car's rest frame and the outside observer's rest frame); but you also need length contraction and relativity of simultaneity to do that.

 

[Meir Achuz]

If the two times are simultaneous in the rest system, they will not be simultaneous in any other system.

 

[powermind]

Thanks very much for your answer.
I did not mean from "at the same time" the simultaneous but at the same duration (delta t)
Suppose A is car'a front end and B is car's back end. In the car, the pules travels from A to B in 1ms for example. It must travel from B to A in 1ms for sure. But for outside observer, he will see that the first pulse hits B in 2ms for exmple becuse it travels longer. And the second pulse hits A in 0.5ms because it travels shorter. But when we apply time dilation T=t/sqrt(1-v2/c2) that exectaion is wrong.
Why , on train example, the outside opserver see that the pulse travels from bottom to the top in same duration time (delta t) of traveling from top the bottom.
Train example figure:

Regards,

 

[Nugatory]

But when we apply time dilation T=t/sqrt(1-v2/c2) that exectaion is wrong.

You have to allow for relativity of simultaneity and length contraction as well as time dilation.

 

[powermind]

For more clarification,
From the time dilation equation, the outside opserver can expect how the time is in the car. So if the driver says that the pulse moved from end to end in 1ms, by applying the equation the outside opserver can detect the duration time in his clock. And since the input values of two cases are the same the output values have to be the same.
Otherwise, in the car there are two different clocks not working simultaneously. One of them is in the back and the other is in the front.

 

[PeterDonis]

From the time dilation equation, the outside opserver can expect how the time is in the car. So if the driver says that the pulse moved from end to end in 1ms, by applying the equation the outside opserver can detect the duration time in his clock. And since the input values of two cases are the same the output values have to be the same.

No, they don't, because time dilation is not the only factor involved. There is also relativity of simultaneity, as Nugatory pointed out.

Otherwise, in the car there are two different clocks not working simultaneously. One of them is in the back and the other is in the front.

Exactly. The two clocks both tick at the same rate, according to the outside observer, but their "zero points" are not the same according to the outside observer. The clock at the back registers a given time reading *before* the clock in the front, according to the outside observer. Consider what that means for the time readings as seen by the outside observer: he assigns times to the events as follows:

(1) The back end emits its light pulse; this event is at time $t_0$ according to the observer in the car, and time $T_A$ according to the outside observer.

(2) The front end emits its light pulse; this event is at time $t_0$ according to the observer in the car, but time $T_B > T_A$ according to the outside observer.

(3) The back end receives its light pulse; this event is at time $t_0 + t$ according to the observer in the car, but time $T_C$ according to the outside observer.

(4) The front end receives its light pulse; this event is at time $t_0 + t$ according to the observer in the car, but time $T_D > T_C$ according to the outside observer.

Now: by time dilation, the time interval $t$ according to the observer in the car equates to a time interval $\gamma t$ (where $\gamma = 1 / \sqrt{ 1 - v^2 / c^2}$) according to the outside observer. So the time intervals between events #1 and #3, and between events #2 and #4, will be equal to $\gamma t$ according to the outside observer: i.e., $T_C = T_A + \gamma t$ and $T_D = T_B + \gamma t$.

However, the time it takes for the light pulse emitted at the back of the car to travel to the front, according to the outside observer, is $T_D - T_A$, which will be *larger* than $\gamma t$, because $T_A < T_B$. And the time it takes for the light pulse emitted at the front of the car to travel to the back, according to the outside observer, is $T_C - T_B$, which will be *smaller* than $\gamma t$, because $T_B > T_A$. So to get the correct time intervals according to the outside observer, you have to take into account relativity of simultaneity as well as time dilation.

 

[powermind]

In your last example, does the pulse return back? I mean that the interval t is from A to B and back to A?

 

[PeterDonis]

In your last example, does the pulse return back? I mean that the interval t is from A to B and back to A?

The way I set it up, one pulse goes from the back to the front (A to B), and one goes from front to back (B to A), and they cross in the middle.

However, it's easy enough to change things around to have a single pulse that is reflected, and the answer is the same: the times are different according to the outside observer.

Suppose the pulse starts at the back of the car; then it corresponds to the pulse going from event #1 to event #4 in my previous post, taking time $T_D - T_A > \gamma t$. The reflected pulse then starts at event #4 and ends at a new event:

(5) The back of the car receives the reflected pulse: this happens at time $t_0 + 2 t$ according to the observer in the car, but at time $T_E$ according to the outside observer.

However, we also know the following: according to the outside observer, the time between event #4 and event #5 is the same as the time between events #2 and #3 in my previous post (since events #4 and #5 are just events #2 and #3 translated forward in time by the same amount). So we have $T_E - T_D = T_C - T_B < \gamma t$, i.e., the reflected pulse (front to back) takes less time to travel, according to the outside observer, than the forward pulse (back to front).

 

[powermind]

I read your answer many times to understand. but sorry I am confused so please be patient
You do say in post #2:

However, in a frame in which the car is moving at speed v, the pulse from the car's back end will be sent first, before the pulse from the car's front end; but the pulse from the car's front end will be *received* first (at the car's back end), *before* the pulse from the car's back end is received at the car's front end.

This mean $T_D$ should be before $T_C$. Am I right? if so why you said in post #7 that $T_D$ > $T_C$?

one more questions please:
How can we determine which part should be before than other?
In more details, suppose there is a vehicle in square shape and has four light sources in each corner. While the vehicle is moving, the four lights are switched on at the same time according to the driver. Can you determine for outside observer the first light source that is switched on and the second and so on.

Best regards

 

[PeterDonis]

This mean $T_D$ should be before $T_C$. Am I right?

No. $T_C$ is the time when the pulse from the front end is received at the back end; $T_D$ is the time when the pulse from the back end is received at the front end. So $T_D > T_C$, as I said.

How can we determine which part should be before than other?

The best general method is to draw a spacetime diagram; it's usually easier to see the relationships between events visually.

The other general method is to pick a frame where you can assign coordinates to all events from the statement of the problem, and then use the Lorentz transformation to figure out the coordinates of events in any other frame of interest.

In more details, suppose there is a vehicle in square shape and has four light sources in each corner. While the vehicle is moving, the four lights are switched on at the same time according to the driver. Can you determine for outside observer the first light source that is switched on and the second and so on

It depends on how the car is moving. If it is moving exactly forward, i.e., exactly perpendicular to one face, then the rear lights (the two in the corners on the rearward face) will be switched on first according to the outside observer (and both will be switched on at the same time), and the front lights (the two in the corners on the front face) will be switched on second.

 

[powermind]

Thank you very very much. It is clear for me now. Let me study it carefuly.Regards,

 

[powermind]

If it is moving exactly forward, i.e., exactly perpendicular to one face

In the same example, if there are many light sources located as a line from the back to the front. The all sources are switched on at the same time according to the driver. For outside observer, the light at the back end will be switched on first then the next light and so on. The light at the front end will be the last turn. Is this true?

It depends on how the car is moving

Suppose the outside observer stands on middle of street and the car is moving to hit him. The front and rear lights of the car are switched on at the same time according to the driver. Which light will be seen first for the outside observer.

I have another good question, I hope, I will write it later depending on above questions.

Regards,

 

[Nugatory]

Suppose the outside observer stands on middle of street and the car is moving to hit him. The front and rear lights of the car lighten simultaneity. Which light will be seen first by the outside observer.

Simultaneously according to who? If you mean that the front and back lights are both switched on at the same time using a frame in which the car is at rest, then the light from the front lights will reach the outside observer before the light from the rear lights..

 

[powermind]

What about the first question in my last post?

 

[PeterDonis]

In the same example, if there are many light sources located as a line from the back to the front. The all sources are switched on at the same time according to the driver. For outside observer, the light at the back end will be switched on first then the next light and so on. The light at the front end will be the last turn. Is this true?

Yes.

Suppose the outside observer stands on middle of street and the car is moving to hit him. The front and rear lights of the car are switched on at the same time according to the driver. Which light will be seen first for the outside observer.

The front light. The reason this answer is different is that it's about something different: it's about when the light is actually *seen* by the outside observer, instead of what time he assigns to the light being *emitted*. He sees the front light first because it has less distance to travel; but he assigns an earlier time to the rear light being emitted because he derives the times of emission for each light by *subtracting* the light travel time from the time he actually sees each light. If you work out the math (or if you draw a spacetime diagram), you will see that the result of this subtraction process will always end up with an earlier time of emission for the rear light according to the outside observer, if the lights are both emitted at the same time according to an observer riding along with the car.

 

[Nugatory]

What about the first question in my last post?

You mean:

In the same example, if there are many light sources located as a line from the back to the front. The all sources are switched on at the same time according to the driver. For outside observer, the light at the back end will be switched on first then the next light and so on. The light at the front end will be the last turn. Is this true?

Note that you've asked a different question here.

In your second question, you asked when the light reaches the eyes of the outside observer, while here you' re asking when the light source is switched on according to the outside observer, which is to say, when the light starts its journey to his eyes.

But with that said, yes, if the lights go on simultaneously according to the car observer, they will on back to front according to the outside observer.

 

[powermind]

The reason this answer is different is that it's about something different: it's about when the light is actually *seen* by the outside observer, instead of what time he assigns to the light being *emitted*. He sees the front light first because it has less distance to travel; but he assigns an earlier time to the rear light being emitted because he derives the times of emission for each light by *subtracting* the light travel time from the time he actually sees each light. If you work out the math (or if you draw a spacetime diagram), you will see that the result of this subtraction process will always end up with an earlier time of emission for the rear light according to the outside observer, if the lights are both emitted at the same time according to an observer riding along with the car.

I am afraid if I do not understand very well but let me say something.
Considering on the distance brtween the outside opserver and the lights, also if the car is not moving, the outside observer will see the front light before rear one. Here I confused since you said that the $T_B$>$T_A$. I did not ask before why $T_B$>$T_A$? But now I would like to find the answer. Is there any provement and is it only for special position or any position in the frame which the car is moving?

Regarding the example of lights on a line, any delay of a light respect to other in same car to be switched on causes that no light should be switched on! This is phylosophy I will explain it more later.

 

[PeterDonis]

if the car is not moving, the outside observer will see the front light before rear one.

Yes, he will *see* the front light before the rear one; but if the car is not moving, the outside observer will say that the two lights were both *turned on* at the same time. He sees the front one first because its light has a shorter distance to travel.

Here I confused since you said that the $T_B$>$T_A$.

If the car is moving, yes. If the car is not moving relative to the outside observer, then $T_B = T_A$.

I did not ask before why $T_B$>$T_A$?

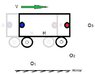
Suppose we have an observer riding in the car exactly halfway between the front and rear lights. Call this observer M. Then the front and rear lights are turned on simultaneously, relative to the car, if observer M receives the light from both lights at the same instant (i.e., the same event).

Now, suppose there is an observer who is at rest relative to the outside observer, and who is co-located with observer M at the instant when the light from both car lights (front and rear) arrives. Call this observer O. If the car is not moving, then observer O is co-located with observer M for all time; so he will assign the same times to the two lights being turned on as observer M does, because he can use the same reasoning that observer M does: both lights are the same distance from him, and he sees the lights at the same instant, so they must have been turned on at the same instant. So if the car is not moving, $T_A = T_B$.

But now suppose instead that the car is moving. Observer O will still see both lights at the same instant, because he is co-located with observer M at that instant. But now he will reason that the light at the rear of the car, which is moving towards him, must have been turned on first, because its light will have had to travel a greater distance to get to him than the light from the front of the car, which is moving away from him. And since observer O is at rest relative to the outside observer, the outside observer will assign the same time relationships (earlier and later) between events as observer O does. So if the car is moving, then $T_A < T_B$.

Here's another way of seeing it: take into account that, according to observer O, observer M is moving relative to the light emitted from the front and rear of the car. Observer O will reason that the light emitted from the rear of the car has to travel further to catch observer M, since observer M is moving away from that light (i.e., observer M, according to observer O, is moving in the same direction as the light); whereas the light emitted from the front of the car is moving towards observer M (i.e., in the opposite direction to observer M, according to observer O), so it doesn't have to travel as far. So for both light beams to reach observer M at the same instant, the light from the rear of the car must have been emitted first according to observer O, i.e., $T_A < T_B$.

 

[powermind]

I do not understand well! Is the delay because of the distance between O and the light sources or because of the car moving?

Anyway, please see this figure:

There is a possilbe location outside the car so that the observer in this location will find that $T_B$ equals $T_A$!

another point, you said:

However, the time it takes for the light pulse emitted at the back of the car to travel to the front, according to the outside observer, is $T_D$−$T_A$, which will be *larger* than γt , because $T_A$<$T_B$. And the time it takes for the light pulse emitted at the front of the car to travel to the back, according to the outside observer, is $T_C$−$T_B$, which will be *smaller* than γt , because $T_B$>$T_A$. So to get the correct time intervals according to the outside observer, you have to take into account relativity of simultaneity as well as time dilation

On the contrary for observer O3, $T_D$−$T_A$ will be smaller than γt and $T_C$−$T_B$ will be larger than γt!
I think this is not true because the distance between A and D should be greater than the distance between B and C!

Regards,

 

[Nugatory]

I do not understand well! Is the delay because of the distance between O and the light sources or because of the car moving?

The relativistic effects (length contraction, time dilation, relativity of simultaneity) depend only on the relative speed of the various observers.

The delay between when a light signal leaves the source and when it reaches an observer depends only on the distance between the point of emission and the point of detection. The relative speed of the source and the observer makes no difference (except that if the observer is moving it may be harder to see exactly where the point of detection will be). However, that distance will be affected by length contraction, so different observers moving at different speeds relative to one another will find that the distance, and hence the time that the light takes to cross that distance, are different.

There is a possilbe location outside the car so that the observer in this location will find that $T_B$ equals $T_A$!

You can find locations outside the car where the light from A and B reaches the observer at the same time. However, if the observer is moving relative to the car, the distance covered by the two flashes will be different, and the observer will therefore conclude that the two flashes left their sources at different times. You will not be able to find any position at which both flashes will reach an observer at rest outside the moving car at the same time AND have covered the same distance AND were simultaneous according to the observer in the car.

On the contrary for observer O3, $T_D$−$T_A$ will be smaller than γt and $T_C$−$T_B$ will be larger than γt!
I think this is not true because the distance between A and D should be greater than the distance between B and C!

I've said it before, and I'll say it again: you have to allow for the relativity of simultaneity and length contraction, not just time dilation, to make it all come out right.

 

[jartsa]

Hi,
Car is moving at speed v. The pulse is sent inside from the back to the front. It takes time t. Another pulse is sent from the front to the back and takes same t. How should outside observer expect? Does he find that the two pulse hit sides at the same time? It sounds no. How can you apply time dilation equation for this example?

Well how about deriving the correct equations and then applying those equations.

Let's make the car to move at non-relativistic speed v=0.1 c. Now calculate the time difference according to the outside observer, ignoring relativistic effects.

 

[PeterDonis]

There is a possilbe location outside the car so that the observer in this location will find that $T_B$ equals $T_A$!

No, there isn't, because $T_A$ and $T_B$ have nothing to do with when the outside observer *sees* the light beams from the front and rear of the car; they are the times that the outside observer assigns to the light beams being *emitted* at one end of the car (or *received* at the other end of the car if we include $T_C$ and $T_D$). The relationships between those times are as I said in my previous post, regardless of where the outside observer is located. Please re-read my posts, carefully.

 

[PeterDonis]

You can find locations outside the car where the light from A and B reaches the observer at the same time.

Yes, but note that that's not what $T_A$ and $T_B$ mean, or $T_C$ or $T_D$. Those are the times assigned by the outside observer to the light beams being emitted or received at the front or rear of the car. They are unaffected by the outside observer's location.

 

[Nugatory]

Yes, but note that that's not what $T_A$ and $T_B$ mean, or $T_C$ or $T_D$. Those are the times assigned by the outside observer to the light beams being emitted or received at the front or rear of the car. They are unaffected by the outside observer's location.

I agree - that's (supposed to be) what the chain of ANDs in the next sentence is about.

 

[powermind]

Hi again,
The discussion is going to be complicated for me. So, I would like to simplify it.
1. We will ignore the length change till I understand the concept.
2. We will focus on the time that the light switched on at.

See this example:

In the example, there are three outside observers O1, O2 and O3 who are not moving while the observer M is in the vehicle which is moving forward. There are two lights at back and front of the vehicle. The lights are switched on at the same time according to M.

- $T_A1$ is the reached time of the back light beam to O1’s eyes.
- $T_B1$ is the reached time of the front light beam to O1’s eyes.
- $T_A2$, $T_B2$, $T_A3$ and $T_B3$ for other observers O2 and O3 respectively.

The first questions are:
1. Do the outside observers share same clock? I think yes 
2. You said that O1 will find $T_B1$>$T_A1$, and O3 will find $T_B3$<$T_A3$:

a. What is the comparison between $T_A1$ and $T_A3$ and the comparison between $T_B1$ and $T_B3$? Greater, smaller or equal?
b. If O3 sees the mirror located behind O1, he will see the back light first definitely like O1. This is a strange? Is not this?
c. $T_B1$>$T_A1$! Is it because of the distance between the light source and the observer O1? If so, imagine another light located in the middle of the vehicle between back light and front light. Its distance could be shorter than the distance of the back light. Hence, O1 should see the middle light before the back light but you said the opposite!​

 

[Dale]

The discussion is going to be complicated for me. So, I would like to simplify it.

This is your idea of simplification? This is very complicated.

1. We will ignore the length change till I understand the concept.

You cannot always ignore it. However, you can do things like specify the length of the car in the O frame.

2. We will focus on the time that the light switched on at.

Here you say that you will focus on the time that the light switched on, but your questions below are about the time that the light is seen. Those are different things.

The lights are switched on at the same time according to M.

For simplicity, let's use units of length such that the car is length 2 in the O frame and let's use units of time such that c=1. In that case in the O frame A switches on at t=-v and B switches on at t=v.

1. Do the outside observers share same clock? I think yes 

I wouldn't say that they share the same clock, I would say that their clocks are synchronized.

2. You said that O1 will find $T_B1$>$T_A1$, and O3 will find $T_B3$<$T_A3$:

a. What is the comparison between $T_A1$ and $T_A3$ and the comparison between $T_B1$ and $T_B3$? Greater, smaller or equal?​

$T_A1=-v+\sqrt{1+y_1}$ and $T_A3=1-v+x_3$, so the comparison depends on the exact values of $y_1$ and $x_3$ and v. Similarly with B.

b. If O3 sees the mirror located behind O1, he will see the back light first definitely like O1. This is a strange? Is not this?

If the mirror is located at y=d/2 then $T_{AM}3=-v+\sqrt{1+d^2+2x_3+x_3^2}$ and $T_{BM}3=v+\sqrt{1+d^2-2x_3+x_3^2}$, so it is not true that O3 will definitely see the reflected back light first. Again, it depends on the exact values of d and $x_3$ and v.

c. $T_B1$>$T_A1$! Is it because of the distance between the light source and the observer O1?

In the O frame those distances are equal and the reason that $T_B1$>$T_A1$ is simply because A switched on before B.

 

[powermind]

DaleSpam, the main problem is why you assume that A is switched on before B according to O!
Is there a logical answer not bring us back to the last post?

Regards,

 

[Dale]

DaleSpam, the main problem is why you assume that A is switched on before B according to O!

I didn't assume it. You specified:

The lights are switched on at the same time according to M.

So, if the car length is $L_0$ in the M frame then that means A switches on at $t'=0$ and $x'=-L_0/2$ and B switches on at $t'=0$ and $x'=L_0/2$. If you Lorentz transform that to the O frame and choose units such that $L_0=2\sqrt{1-v^2}$ then you get the results I posted above.

It wasn't an assumption I made, it was a result derived from your specification that they were switched on at the same time according to M.

 

[Nugatory]

DaleSpam, the main problem is why you assume that A is switched on before B according to O!
Is there any logical answer?

Take the distance between the point where A was when it was switched on and where O was when the light from A hit his eyes.

Take the distance between the point where B was when it was switched on and where O was when the light from B hit his eyes.

If those two distances are different and both light flashes reached O's eyes at the same time, then either the two flashes did not start at the same time according to O, or the two light signals traveled at different speeds. There's no other way for them to have covered different distances yet have arrived at the same time. There's enough empirical evidence to reject the "light traveled at different speeds", so we're left with the two light signals have started at different times.

You've also specified that the two flashes of light traveled the same distance to get to M's eyes, and both flashes arrived at his eyes at the same time. Thus, they were simultaneous according to M.