Thermal (PV) Diagram: Calculating Work, Heat Transfer & Entropy

[forty]

Consider the cycle shown below for n moles of an ideal gas. The gas has a heat capacity of C_v=(3/2)nR and is initially at a temperature T₀, a pressure P₀ and a volume V₀. The process a->b consists of a quasistatic, isobaric expansion to twice the initial volume. The process b->c consists of a quasistatic, isochoric decrease in pressure and the process c->a is a quasistatic , adiabatic compression.

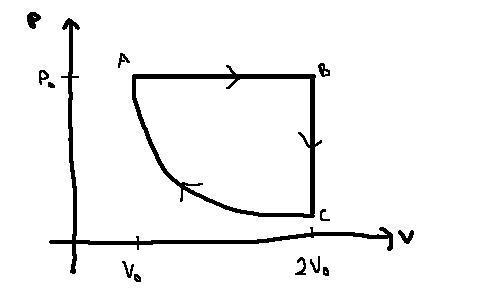
(a) In terms of the initial pressure at point a, P₀, what is the pressure at the point c?

Worked this out to be P_c = 2^-ɣP₀

(b) In terms of the initial temperature at point a, T₀, what is the temperature at points b and c.

Worked these out to be T_b = 2T₀ and T_c = 4^-1/fT₀

(c) Construct a table which displays for each of the three processes in this cycle:
The work done, the heat transfer, the change in internal energy, the change in enthalpy and the change in entropy. Express your answers in terms of R, the universal gas constant, n, the number of moles of the gas present and T₀, the initial temperature at point a.

For a->b:

Work done: W=-PΔV=-P₀(2V₀-V₀)=-P₀V₀=nRT₀

Heat transfer: 0?

Change in internal energy: (f/2)nRΔT=(f/2)nR(T_b-T_a)=(f/2)nR(2T₀-T₀)

Change in enthalpy: ΔH=ΔU+PΔV=(f/2)nR(4^-1/fT₀-2T₀)+nRT₀

Change in entropy: ΔS=nRln(V_f/V_i)=nRln(2)

For b->c:

Work done: 0

Heat transfer: Does this = ΔU?

Change in internal energy: ΔU=(f/2)nRΔT=(f/2)nR(T_c-T_b)=(f/2)nR(4^-1/fT₀-2T₀)

Change in enthalpy: ΔH=ΔU+ΔPV=(f/2)nR(4^-1/fT₀-2T₀)+0

Change in entropy: ΔS=nRln(V_f/V_i) Does this work here?

I'm just not sure if I'm on the right track... Especially for part (c). Any help with this would be appreciated.

 

[Redbelly98]

Congrats on reaching 100 posts

(a) looks good, though they probably want you to use the actual value of γ to calculate a completely numerical value x P_o.

(b) I agree with Pb, but get something else for Pc. Also, what is f? I'm not familiar with that quantity.

(c)

W_ab: it's nRT_o for work done by the gas, or -nRT_o done on the gas. Not sure which convention you're using.

Q_ab is not zero. Path a-b is not adiabatic.

ΔU_ab: Since U = (3/2) nRT, and you know the temperatures, this is pretty straightforward. Again, not sure what f is (is it 3?). Also, there is an obvious simplification for the expression (2T_o-T_o)

I'm going to stop here for now. If you work out the above stuff, then we can continue with the rest.

 

[forty]

f is the number of degrees of freedom, so f = 3.

and for P_c I had the power up the wrong way.. I end up with P_c = T₀/root(8) does this look better?

So as you said Q_ab is not 0. But ΔU_ab = (3/2)nRΔT and

ΔT=T₀ so ΔU_ab = (3/2)nRT₀. Then can you use this to

solve for Q_ab? U=Q+W so (3/2)nRT₀=-nRT₀+Q =>

(Our convention is that W=-PΔV)

Q=(5/2)nRT₀


So how am I going now?

 

[Redbelly98]

f is the number of degrees of freedom, so f = 3.

Okay, got it.

and for P_c I had the power up the wrong way.. I end up with P_c = T₀/root(8) does this look better?

(Guess you meant T_c here.)
Not quite, it looks like something happened with the exponent on 2. I.e., it's not 2^-3/2T₀ as you have, but the correct answer does not look very different from 2^-3/2T₀.

So as you said Q_ab is not 0. But ΔU_ab = (3/2)nRΔT and

ΔT=T₀ so ΔU_ab = (3/2)nRT₀. Then can you use this to

solve for Q_ab? U=Q+W so (3/2)nRT₀=-nRT₀+Q =>

(Our convention is that W=-PΔV)

Q=(5/2)nRT₀

Yes.

 

[forty]

don't tell me T_c=2T₀

My logic for this is..

P_iV_i^ɣ=P_fV_f^ɣ

then replacing P with T using the ideal gas law => P=nRT/V

T_iV_i^ɣ-1=T_fV_f^ɣ-1

but V_i = V_f so they just cancel? which leaves T_i=T_f and T_i=T_b and T_f=T_c so T_c=T_b

But if the Volume is constant and the pressure is changing then the temperature must change. What am I doing wrong? Maybe its just late and I can't think properly.

 

[Redbelly98]

Be careful. Which path are you talking about, a-c or b-c?

If you mean path a-c, then

V_i ≠ V_f​

Or if you meant b-c, then

P_iV_i^γ ≠ P_fV_f^γ​

Perhaps use subscripts a, b, c instead of i, f so that it is clearer.

 

[forty]

How does T_c=2^-2/3T₀ look?

using V_aT_a^f/2=V_cT_c^f/2

 

[Redbelly98]

How does T_c=2^-2/3T₀ look?

Looks good!

 

[forty]

One last question!

If this cycle is operated as a heat engine, what would be its efficiency?

From memory this is 1 - T_c/T_h

There T_c is the temp of the cold reservoir and T_h the temp of the hot reservoir.

I have no idea on where to start for this.

 

[Andrew Mason]

One last question!

If this cycle is operated as a heat engine, what would be its efficiency?

From memory this is 1 - T_c/T_h

There T_c is the temp of the cold reservoir and T_h the temp of the hot reservoir.

I have no idea on where to start for this.

This is not a Carnot engine. So:

$$\eta = W/Q_h =1-Q_c/Q_h \ne 1-T_c/T_h$$

You have to determine the heat flow into the gas in a->b and b->c to find Qh. You then have to calculate W (the area under a->b minus the area under c->a).

AM

 

[forty]

So that means I need to know the answer to the following (what this originally started as)

Construct a table which displays for each of the three processes in this cycle:
The work done, the heat transfer, the change in internal energy, the change in enthalpy and the change in entropy. Express your answers in terms of R, the universal gas constant, n, the number of moles of the gas present and T0, the initial temperature at point a.

(C_v=(3/2)nR)

Now I've cleared up some problems let see if i can get this right!

So a->b

Work done W_ab: Just area under the graph P₀V₀=-nRT₀

Change in internal energy U_ab: (3/2)nRΔT = (3/2)nRΔT = (3/2)nRT₀

Heat transfer Q_ab: Using U=Q+W (know U and W) => Q_ab=(5/2)nRT₀

Change in enthalpy ΔH_ab: ΔH=ΔU+PΔV=(5/2)nRT₀

change in entropy ΔS_ab: ΔS=nRln(V_b/V_a)=nRln(2) (I'm not sure this works when the internal energy changes)
Or can I use the fact that its at constant pressure so ΔS = Integral(T_a->T_b) C_p/T dT ?


So b->c

Work done W_bc: Area under graph = 0

Change in internal energy U_bc: For this can I use an integral from T_b to T_c I get an answer of (3/2)nRT₀(2^-2/3-2) Is this right?

Heat transfer Q_bc: As W = 0, ΔU=ΔQ so Q just is the same as above? (3/2)nRT₀(2^-2/3-2)

Change in enthalpy ΔH_bc: ΔH=ΔU+ΔPV Can I use this? Or is it just the change in Q? ΔH=(3/2)nRT₀(2^-2/3-2)

change in entropy ΔS_bc: ΔS=C_v/T dT Can I use this here as well?


So c->a

Heat transfer Q_ca: This is 0 as it's adiabatic.

Change in internal energy U_ca: ΔU=(3/2)nR * Integral(T_c->T_a) 1 dT = (3/2)nRT₀(1-2^-2/3) I have a feeling this is very wrong.

Work done W_ca: As Q = 0 then W=U so ΔW=(3/2)nRT₀(1-2^-2/3)

Change in enthalpy ΔH_ca: No idea.

change in entropy ΔS_ca: Is this 0?

Now if any of this is even remotely correct does Q_h = Q_ab+Q_bc = (5/2)nRT₀ + (3/2)nRT₀(2^-2/3-2)

And the work done W = nRT₀ - (3/2)nRT₀(1-2^-2/3)

I'm very sketchy on all of this, especially c->a. I can understand if you are over helping me with this but either way thanks for all the help!

 

[Andrew Mason]

You have the right idea. For c->a the work done is equal in magnitude to the change in internal energy, since there is no heat flow.

$$W_{ca} = -\Delta U = nC_v(T_a-T_c)$$

$$T_c = T_a(2)^{1-\gamma}$$, so:

$$W_{ca} = -nC_v(T_a(1-(2)^{1-\gamma})$$

Add that to your answer for the work done from a->b to get the total work (be careful about the signs. Wca is negative and Wab is positive).

AM

 

[Redbelly98]

I agree with the calculations for ΔU, W, and Q for each process. I'm not sure about ΔH and ΔS, I would have to review that or maybe Andrew can comment on it. (ΔS is definitely 0 for c-a, the adiabatic process.)

As for efficiency, I agree with

the work done W = nRT0 - (3/2)nRT₀(1-2^-2/3)

(though strictly speaking this is -W.)

As for Q_h, only those processes with Q>0 will contribute to the calculation of Q_h. So you need to check which of Q_ab and Q_bc are positive.

EDIT: didn't see Andrew's recent post before posting this ... had this window open for more than an hour before I got around to composing my response

 

[Redbelly98]

Add that to your answer for the work done from a->b to get the total work (be careful about the signs. Wca is negative and Wab is positive).

AM

Hi Andrew,

FYI, in forty's class they define

W = -∫P dV​

i.e., it's the work done on the gas.

$$W_{ca} = -nR(T_a(1-(2)^{1-\gamma})$$

Is there a 3/2 factor missing? (Or maybe I am missing something?)

 

[Andrew Mason]

Is there a 3/2 factor missing? (Or maybe I am missing something?)

Redbelly,

Yes. Thanks for noticing that. That should be Cv not R. The internal energy change from c->a is:

$$\Delta U = nC_v(T_a(1-(2)^{1-\gamma}) = \frac{3nR}{2}(T_0(1-(2)^{-2/3})$$

AM

 

[Andrew Mason]

I agree with the calculations for ΔU, W, and Q for each process. I'm not sure about ΔH and ΔS, I would have to review that or maybe Andrew can comment on it. (ΔS is definitely 0 for c-a, the adiabatic process.)

The entropy calculation is:

$$\Delta S_{total} = \Delta S_{ab} + \Delta S_{bc} + \Delta S_{ca}$$

For a->b, P is constant so dQ = nC_pdT

$$\Delta S_{ab} = \int_{T_a}^{T_b} dQ/T = nC_p \int_{T_a}^{T_b} dT/T = nC_p\ln\left(\frac{T_b}{T_a}\right)$$

For b->c, V is constant, so dQ = dU = nCvdT

$$\Delta S_{bc} = nC_v\int_{T_b}^{T_c}dT/T = nC_v\ln\left(\frac{T_c}{T_b}\right)$$

For c->a, Q = 0 so there is no change in entropy (dQ/T = 0).

AM

 

[forty]

So for my efficiency I need W/Qh

So work = -nRT0 - (3/2)nRT0(1-2^-2/3)

And Qh is just Qab as Qbc is negative so I get

(-nRT0 - (3/2)nRT0(1-2^-2/3) ) / (5/2)nRT0

How does this look?

 

[forty]

Anyway guys thanks for all the help, really is appreciated!

 

[Redbelly98]

You had the correct work done by the gas earlier,

And the work done W = nRT₀ - (3/2)nRT₀(1-2^-2/3)

Looks like you got a "-" sign error in your post #17. If you correct that, you'll be close ... but will need to simplify the expression further.

 

[forty]

( nRT₀ - (3/2)nRT₀(1-2^-2/3) ) / (5/2)nRT₀

Is right it just needs to be simplified?

If i simplify i get an answer of (2/5)-(3/5)(1-2_-2/3)=.1779

Please tell me I am right >.<

 

[Redbelly98]

Yes.

 

[forty]

I can now actually say thanks for the help, all done! Really thanks again it is appreciated!