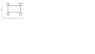portofino
- 35
- 0
Homework Statement
Determine the efficiency for the cycle shown in the figure, using the definition. Assume that the gas in the cycle is ideal monatomic gas.
Compare with the efficiency of a Carnot engine operating between the same temperature extremes.
see attachment
Homework Equations
the cycle is composed of two isobaric and two isovolumetric paths.
isovolumetric/constant volume:
work, W = 0
heat, Q = deltaU = nC_v(deltaT) where deltaU is change in internal energy, n is number of moles, C_v is constant volume (monotomic so = 3R/2 where R = 8.314), delta T is change in temp
isobaric/constant pressure
work, W = p(V_2 - V_1) where p is pressure in pascals, V_2 is final volume, V_1 is initial volume
heat, Q = deltaU + W = nC_p(deltaT) where C_p is constant pressure = C_v + R
ideal gas law: PV = nRT
efficiency, e = W/Q_h = (Q_h - Q_c)/Q_h = 1 - (Q_c/Q_h) where W is work, Q_h is heat energy (high), and Q_c is cool heat energy (low)
The Attempt at a Solution
i intend to use efficiency, e = W/Q_h, since W = 0 for each of the two isovolumetric paths, the work only comes from the two isobaric paths, i calculated:
top horizontal path to be W = 2431.8 joules, and the bottom horizontal path to be W = 1215.9 joules, so net work would be W_net = 3647.7 joules
now in order to solve for Q_h or even Q_c for that matter I need to be able to solve for heat Q, in order for that i need to know the number of moles and the temp in kelvin.
since i am only concerned with Q_h, do i only need to know the heat energy Q from the top horizontal (isobaric) path?
so Q = nC_p(deltaT) and using ideal gas law and solving for T and subsituting in for T is the constant pressure heat equation i get:
Q = nC_p(PV/nR) so the n's cancel out, and C_P = C_v + R = 3(8.314)/2 + 8.314 = 20.785, here is where i am confused. since the top horizontal path is isobaric, the volume changes thus what volume do i use for V?
so currently my equation for Q would be Q = nC_p(PV/nR) = 20.785[((607950Pa)(V))/8.314]
any help/clarification appreciated