Thevenin Problem Homework: Find Current When RL is Short

[erok81]

Homework Statement

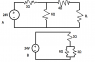
This one has a few parts, so let's start with part a. See attachment for circuit. I've got two drawings in the attachment. I'll label them A and B. Image A is the original circuit.

Homework Equations

None.

The Attempt at a Solution

My first step is to find set R_L to open. I can use a voltage divider equation and find the voltage to be 16V.

The next (which is where I am stuck) is to find R_L as a short. Shown by image B. My professor wasn't the best in showing this as he used some trick I have no clue how solved this way.

I can find I_TOT using...

I=\frac{V}{R} \Rightarrow \frac{24}{3+6//4}

Solving for I_TOT gives me 4.4A. My professor used this value and somehow came up with the current over the 4Ω resistor.

Then plugged it into..

R_{th} = \frac{V_th}{I_{short}}

To find the Thevenin equivalent.

How does one find the current when R_L is a short?

 

[Zryn]

Did you mean for the parallel resistors in Diagram B to be 6R and 4R? They are labeled 6R and 3R currently.

Knowing the circuit series current allows you to determine how the current will split when it enters a parallel connection. The general way to do this is using the current divider formula:

I_{n} = I_{s} * \frac{R_{other}}{(R_{other} + R_{n})}

Where:

R_{other} is the total resistance of the other resistors, R_{n} is the resistance which you wish to find the current through, I_{s} is the current being divided and I_{n} is the current you want to find.