Three charges at corners of equilateral triangle

[PseudoGal]

Homework Statement

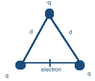
Three point charges q,q and -q lie at three corners of an equilateral triangle of side length d with -q at the apex. If an electron is released from rest midway at the base (point P) what is its KE when its reasonably far away?

Homework Equations

V = kq/r, U = qV

The Attempt at a Solution

I figured out the potential at P. The potential is positive. So the PE of an electron there is negative. If the electron has negative potential energy, why would it move? But Columbs Law predicts that it will move. I am so confused! What does the electron do?

 

[jbriggs444]

Your formula for potential -- it has a factor of "q" in it, right? How do you know whether q is positive or negative?

Edit: Sorry, the above suggestion completely misses your point.

If q is negative then the electron released from rest is attracted to the positive charge at the top of the equilateral triangle. It never gets far away but instead impacts on that top charge.

If q is positive then the electron released from rest is repelled by the negative charge at the top of the equilateral triangle. But, as you point out, its potential energy is negative. It can never get away from the potential well (with a net positive charge) within which it lies.

It appears that the problem was not properly posed. It assumes something that will not actually occur.

 

[PseudoGal]

Thanks Jbriggs. q is positive. So that means the electron has negative potential energy and will not move, correct? They why does Newton's seconds law and Coulumbs Law predict that it will be repelled by the top negative charge and move away from the system? I feel like there is an inconsistency, know what I mean?

 

[jbriggs444]

Negative potential energy does not mean that it will not move. It means that it can not move to infinity (where its potential energy would be zero). It will move. But it cannot move far. Consider the following analogy...

There is an infinite plane. Within this plane there is a valley. Within this valley is a hill. A ball is perched on the side of this hill. It is perched at an elevation that is below the infinite plane but above the bottom of the valley. Does the ball roll down the hill? Yes. Does it roll out of the valley? No.

 

[PseudoGal]

The analogy is definitely helping. Thank you!
So does that mean this situation is not physically possible?
The electric potential at point P is positive, relative to the potential at infinity which is 0. In that sense, the potential energy should decrease and kinetic energy should increase. But since its an electron, does everythign change?

 

[jbriggs444]

The setup is certainly possible. The difficulty is with the question -- "what is its KE when its reasonably far away?". If released from rest, the electron will never get reasonably far away.

[I take "reasonably far" to be shorthand for "infinitely far" without getting into any bother about whether infinity actually exists]

[Edit -- added the following]

The analogy is fairly solid. The electron will seek a low spot where "low" is measured in terms of electrical potential (a positive potential which attracts the electron counts as low and a negative potential which repels the electron counts as high). The hypothetical valley is there because there are two positive charges and only one negative charge. Positive charge = positive potential = low spot. The hypothetical hill is there because within the cluster of charges, the negative charge acts like a hill.

If you want to make the analogy more compelling, make it quantitative. Imagine a rubber sheet with a pair of deep holes pushing down into it and a high pillar pushing up. The holes will look like the ones here http://en.wikipedia.org/wiki/Gravity_well. The hill will be the opposite.

In my mind's eye...

The electron starts sitting at a kind of saddle point between the holes. The existence of the hill means that the sheet slopes down away from the hill. The existence of two holes and only one hill means that the whole area is a bit below where the sheet would otherwise have been.

The electron will ride down the centerline of the saddle until it finds a point where the downslope from the hill dies out and the upslope to the surrounding level region begins. It will oscillate back and forth around this minimum point for potential energy.

If q is negative then instead of two holes and a hill you have two hills and a hole. The electron never gets very far away because it falls into the hole.