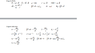Flop880
- 4
- 0
Homework Statement
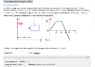
Problem is attached
Homework Equations
A formula sheet is also attached
The Attempt at a Solution
flux=\intB dA from .31m to .82
B=u I(enclosed)/2(pi)(d)
d=x
dA=dx L
so ∫ (u)(I)(L)dx / 2(pi)(x) from .31m to .82m remember x=d in the pic. My answer is 3.9687e-7 and its wrong
integral came out to be (u)(I)(L)/2pi (ln(.82) - ln(.31))
u=4(pi)e-7
I=4A